Решение. Для нахождения точек перегиба надо найти вторую производную данной функции, приравнять ее к нулю и решить полученное уравнение
Для нахождения точек перегиба надо найти вторую производную данной функции, приравнять ее к нулю и решить полученное уравнение. Корни этого уравнения – это критические точки второго рода или точки возможного перегиба. Найдем первую производную
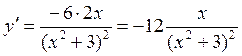
теперь найдем вторую производную
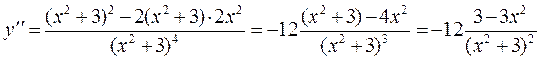
приравнивая вторую производную к нулю, получим уравнение
3-3x2=0
1-x2=0
откуда x1,2= ±1 – критические точки второго рода
Проверим, действительно ли точки x= ±1 являются точками перегиба. Поскольку для данной функции:
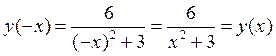 ,
,
то функция четная, значит, если x=1 – точка перегиба, то x= -1 – тоже точка перегиба. Проверим, меняет ли знак вторая производная при переходе через точку x=1. Возьмем, например, x= 0 (-1<0<1) и подставим во вторую производную. Получим 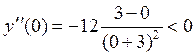 . Возьмем теперь x=2, (2>1), тогда
. Возьмем теперь x=2, (2>1), тогда 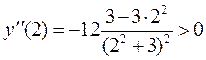 , (вычислять не обязательно, достаточно правильно оценить знак). Поскольку вторая производная меняет знак при переходе через точку x=1, то эта точка есть точка перегиба, но тогда и точка x=-1 – тоже точка перегиба. Ордината обеих точек перегиба будет
, (вычислять не обязательно, достаточно правильно оценить знак). Поскольку вторая производная меняет знак при переходе через точку x=1, то эта точка есть точка перегиба, но тогда и точка x=-1 – тоже точка перегиба. Ордината обеих точек перегиба будет 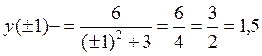 , поскольку точки перегиба лежат на самой кривой. Итак, точки N1(-1;1,5), N2(1;1,5) – точки перегиба графика данной функции
, поскольку точки перегиба лежат на самой кривой. Итак, точки N1(-1;1,5), N2(1;1,5) – точки перегиба графика данной функции
N1(-1;1,5), N2(1;1,5) – точки перегиба
№ 10 Постройте график функции 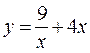 .
.
Дата добавления: 2015-10-13; просмотров: 1302;
