Решение. Найдем производную, приравняем ее к нулю и решим полученное уравнение:

Найдем производную, приравняем ее к нулю и решим полученное уравнение:

y’=12x²+24х

12х²+24х=0

12х(х+2)=0

х=0 или х=-2

Воспользуемся достаточными признаками экстремума и проверим меняет ли знак первая производная при переходе через критические точки от меньших значений к большим. Здесь первая производная существует при любых значениях x. Оценим знаки производной при x=3, x=-1, x=1

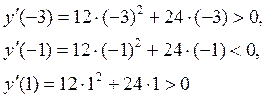
Итак, при переходе слева направо через критическую точку x=-2производная меняет знак с “+” на “–“, то есть функция слева возрастает, а справа убывает. Значит, x=-2 – точка максимума функции. Найдем ее ординату в этой точке:

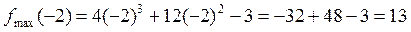
При переходе слева направо через критическую точку x=0 производная меняет знак с “+” на “-”, следовательно, слева убывает справа возрастает, то есть для нее x=0 – точка минимума, причем .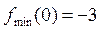

Экстремумы данной функции:

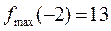
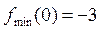
№ 6 Найдите наибольшее и наименьшее значения функции y=x²-x³ на отрезке [-1;3].