Решение. Пример № 8.Вычислить приближенное значение функции y = x3 - 3x2 + 30 при изменении аргумента от 3 до 3,002.

y’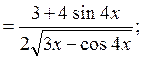

.

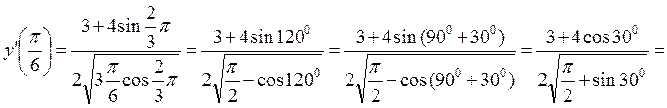
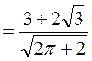Пример № 8.Вычислить приближенное значение функции y = x³ - 3x² + 30 при изменении аргумента от 3 до 3,002.

Решение.

При небольших изменениях аргумента (здесь приращение аргумента ∆x = 3,002-3 = 0,002 небольшое) можно воспользоваться формулой приближенного значения функции f(x₀+∆x)≈f(x₀)+f’(x₀) ∆x Примем f(x) = y = x³-3x² +30, тогда f’(x) = 3x²-6x, положим x₀ = 3, ∆x = 0,002. Вычислим f(x) = 3³-3∙3²+30 = 30; f’(3) = 3∙3²-6∙3 = 9. Тогда, по формуле будем иметь f(3,002) ≈30+9∙0,002 = 30+0,018 = 30,018.