Решение. Эскизное построение графика можно выполнить по общепринятой в анализе схеме.

Эскизное построение графика можно выполнить по общепринятой в анализе схеме.

1 Найдем область определения функции: x ε(-∞,0) U (0, ∞); x = 0 – точка бесконечного разрыва, а прямая x = 0 – вертикальная асимптота кривой.

2 Исследуем функцию на четность (нечетность). Вместо x положим (–x). Получим:

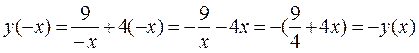, а это признак нечетности функции. Следовательно, ее график центрально симметричен относительно начала координат. Поэтому его можно построить для положительных x и симметрично относительно начала координат перенести для отрицательных x.

3 Найдем точки пересечения графика с осями координат, так называемые “нули” функции. Здесь x≠0 , т.к. x=0 не входит в область определения, значит, с осью O y график не пересекается. Пусть y=0, тогда 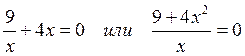. Это равенство невозможно, так как 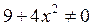при любых значения x. Значит, с осью O y график тоже не пересекается.

4 Найдем точки экстремума и нанесем их на график.

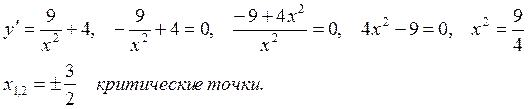
Исследуем характер экстремума в точке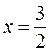

Оценим знаки производной при x=1 и x=2:

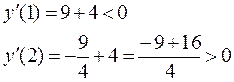, таким образом 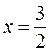– абсцисса точки минимума.

Найдем ординату минимума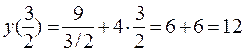

Итак, 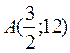– точка минимума.

Но тогда, в силу центральной симметрии, точка 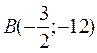– точка максимума.

5 Интервалы монотонности функции:

функция возрастает, если ;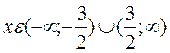

функция убывает, если .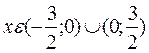

6 Найдем точки перегиба и интервалы выпуклости и вогнутости графика функции 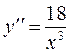и ни при каких значениях x вторая производная не обращается в нуль, а в точке разрыва x=0 функция не определена. Следовательно, график не имеет точек перегиба.

Поскольку при x>0 y’’>0 , то для x ε(0;∞) кривая вогнутая, а для x ε(-∞;0) (в силу симметрии) – выпуклая.

7 По итогам исследования строим график функции y= :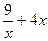

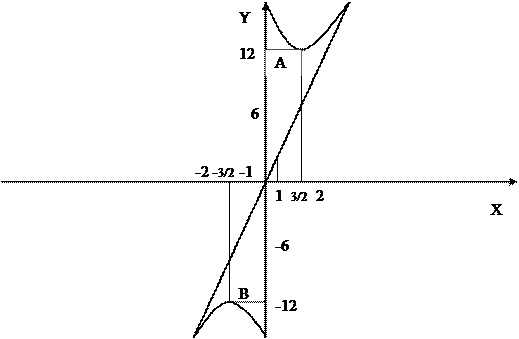
Рисунок 1 График функции y=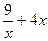

№11 Вычислить приближенное значение функции y=x³-3x²+30 при изменении аргумента от 3 до 3,002.