Алгебраические и трансцендентные функции
В множестве элементарных функций выделяют алгебраические и трансцендентные функции.
Алгебраическими функцияминазывают целые многочлены, рациональные дроби и иррациональные функции.
Например, 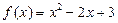 ;
; 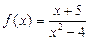 ;
; 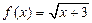 .
.
Трансцендентными функцияминазывают элементарные функции, не являющиеся алгебраическими.
Например, 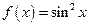 ;
; 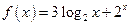 ;
; 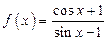 .
.
Среди алгебраических функций выделяются целые многочлены и рациональные дроби.
Целым многочленом (полиномом)степени n относительно переменной x называется функция следующего вида:
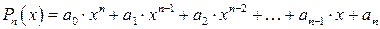 (1)
(1)
здесь 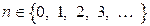 — степень многочлена;
— степень многочлена;
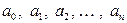 – коэффициенты многочлена (числа или параметры);
– коэффициенты многочлена (числа или параметры);
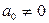 – старший коэффициент.
– старший коэффициент.
Примеры (целые многочлены)
1) 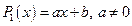 – многочлен первой степени;
– многочлен первой степени;
2) 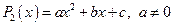 — квадратный трехчлен, или квадратичная функция;
— квадратный трехчлен, или квадратичная функция;
3) 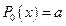 — многочлен нулевой степени;
— многочлен нулевой степени;
4) 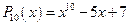 - многочлен 10-й степени.
- многочлен 10-й степени.
График квадратичной функции
Функция 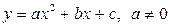 называется квадратичной функцией.
называется квадратичной функцией.
Число 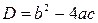 называется дискриминантом квадратного трехчлена.
называется дискриминантом квадратного трехчлена.
Графиком квадратичной функции является парабола, ее положение относительно координатных осей определяется знаком старшего коэффициента a и значением дискриминанта D (см. таблицу на рис. 59).
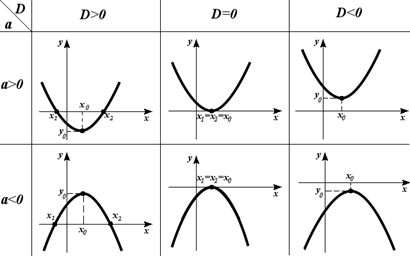
Рис.59
Здесь x1, x2 — это нули квадратичной функции,
вычисленные как корни квадратного уравнения 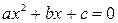 Þ
Þ 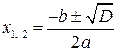 , если
, если 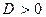 ;
;
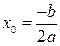 — абсцисса вершины параболы (точка экстремума);
— абсцисса вершины параболы (точка экстремума);
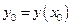 — ордината вершины (экстремум квадратичной функции).
— ордината вершины (экстремум квадратичной функции).
Иррациональные функции— это такие алгебраические функции 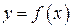 , у которых выражение
, у которых выражение 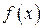 содержит корни различных степеней.
содержит корни различных степеней.
Например, 1) 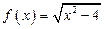 ; 2)
; 2) 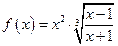 ; 3)
; 3) 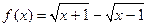 .
.
Дата добавления: 2015-10-19; просмотров: 6950;
