Доказательство. Возьмем полином Жегалкина R для f
Пусть f(x1, . . . , xn) 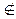 L.
L.
Возьмем полином Жегалкина R для f. Так как f - это нелинейная функция, то в полиноме R содержится слагаемое, включающее произведение некоторых двух переменных. Без ограничения общности можно считать, что такое произведение содержит вхождения переменных x1и x2.
(Если все произведения двух и большего числа переменных не содержат одновременно эти переменные, то необходимо произвести соответствующее переименование переменных в f, используя подстановки переменных вместо переменных функции.)
Сгруппируем слагаемые в R и, вынося переменные x1 и x2 за скобки, представим его в виде
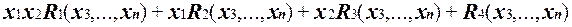 (1).
(1).
Здесь полином R1 содержит хотя бы одно ненулевое слагаемое и поэтому представляет булевскую функцию, отличную от тождественного нуля.
Пусть 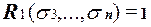 . Подставим вместо переменных x3, . . . , xn конкретные значения
. Подставим вместо переменных x3, . . . , xn конкретные значения 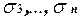 . Тогда имеет место равенство:
. Тогда имеет место равенство:
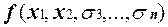 =
= 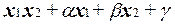 (2)
(2)
Здесь 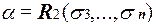 и
и 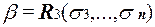 .
.
Заменим x1 на x1 + b и х2 на x2 +a. При этом, если a или b, равно нулю, то соответствующая переменная не заменяется. В противном случае соответствующая переменная заменяется на отрицание этой переменной.
В результате такой замены выражение (2) преобразуется к виду
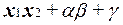 . (3)
. (3)
Если 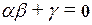 , то функция x1&x2уже получена.
, то функция x1&x2уже получена.
В противном случае применим отрицание к функции вида (3) и также получим x1&x2.
Дата добавления: 2015-09-18; просмотров: 535;
