Доказательство окончено. Рассмотрим применение доказанной леммы к нелинейным функциям.

Рассмотрим применение доказанной леммы к нелинейным функциям.

Пусть f = x₁ ® (x₂ ® x₃). Тогда полином Жегалкина для f имеет вид

f = x₁x₂x₃ + x₁x₂ + 1, т.е. x₁x₂ (x₃ + 1) + 1.

Полином 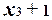равен единице при x₃ = 0. Тогда f(x₁, x₂, 0) = x₁x₂ + 1. Поэтому 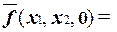x₁& x₂.

Упражнение.

1.Доказать утверждение, обратное утверждению леммы о нелинейной функции.

2. Показать, что всякий из определенных выше классов булевских функций является замкнутым и неполным.