ОПРЕДЕЛЕНИЕ. Множество всех монотонных булевских функций обозначается как M.
Булевская функция f(x1, . . . , xn) называется монотонной, если для любых наборов 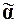 и
и 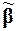 , для которых
, для которых 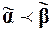 , справедливо неравенство
, справедливо неравенство 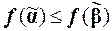 .
.
Множество всех монотонных булевских функций обозначается как M.
Примеры.
1. Функция f (x1, x2)= x1 ® x2 немонотонна, так как
(0, 0) 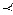 (1, 0), но f(0, 0) > f (1, 0).
(1, 0), но f(0, 0) > f (1, 0).
2. Функции & и 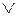 являются монотонными.
являются монотонными.
Множество всех монотонных функций является замкнутым классом. Поскольку тождественная функция f(x) = x - монотонна, то для доказательства замкнутости M достаточно проверить, что при
h = 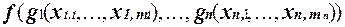 (1),
(1),
где f, g1 ,..., g n - монотонные функции, 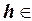 M.
M.
Пусть x1, . . . , xn все различные символы переменных, которые встречаются в формуле (1). Возьмем два набора 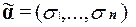 и
и 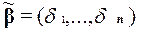 значений этих переменных, для которых
значений этих переменных, для которых 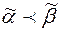 . Тогда для наборов
. Тогда для наборов 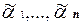 и
и 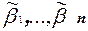 , составленных из значений переменных функций g1, . . . , gn, взятых из наборов
, составленных из значений переменных функций g1, . . . , gn, взятых из наборов 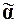 и
и 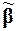 , справедливы соотношения:
, справедливы соотношения: 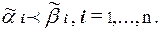
Следовательно, 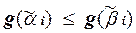 для i = 1, . . . , n. Поэтому
для i = 1, . . . , n. Поэтому 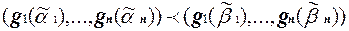 . Поскольку
. Поскольку 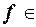 M, то
M, то 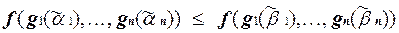 , т.е.
, т.е. 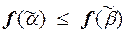 . Поэтому
. Поэтому 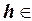 M.
M.
Замечание. Доказанное свойство монотонных функций позволяет просто устанавливать монотонность функций, представленных формулами составленными из монотонных функций. Например, монотонной является функция, представляемая формулой
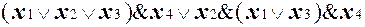 .
.
Простейшей немонотонной функцией можно считать функцию 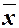 , поскольку три остальные функции одной переменной являются монотонными. Покажем, что отрицание (или простейшая немонотонная функция) может быть получено из всякой немонотонной функции. Последнее свойство можно сформулировать иначе: всякая немонотонная функция содержит отрицание, которое может быть выражено из этой функции.
, поскольку три остальные функции одной переменной являются монотонными. Покажем, что отрицание (или простейшая немонотонная функция) может быть получено из всякой немонотонной функции. Последнее свойство можно сформулировать иначе: всякая немонотонная функция содержит отрицание, которое может быть выражено из этой функции.
Лемма. (О немонотонной функции)
Если 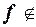 M, то подстановкой вместо переменных этой функции функций-констант и тождественной функции f(x) = x можно получить функцию
M, то подстановкой вместо переменных этой функции функций-констант и тождественной функции f(x) = x можно получить функцию 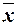 .
.
Дата добавления: 2015-09-18; просмотров: 703;
