САМОДВОЙСТВЕННЫЕ ФУНКЦИИ

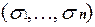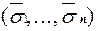Двоичные наборы и называются противоположными наборами.

Противоположные наборы значений переменных в табличном задании булевых функций соответствуют строкам, расположенным симметрично относительно середины таблицы.

Докажем это утверждение. Заметим, что середина таблицы располагается между последним набором верхней половины таблицы (0, 1, . . . , 1) и первым набором значений переменных в нижней половине таблицы (1, 0,. . . , 0).

Тогда, пусть 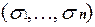и 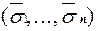- произвольные противоположные наборы. Для определенности будем считать, что s₁ =0.

1. Для набора 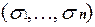, расположенного в верхней половине таблице, определим расстояние до нижнего набора верхней половины таблицы, т.е. количество наборов до набора (0, 1, . . . ,1). Нетрудно видеть, что искомое расстояние представляется числом, имеющим двоичное представление в виде набора .

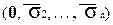2. Определим двоичный набор, находящийся на таком же расстоянии от набора (1,0, . . . , 0), являющегося первым набором нижней половины таблицы

Нетрудно проверить, что 10. . . 0+ = .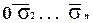

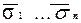Следовательно, набор, отстоящий от (1, 0, . . . , 0) на расстоянии 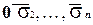, - это набор, который является противоположным 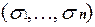. Поэтому расстояния от противоположных наборов 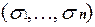и 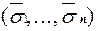до середины таблицы равны.