Задачи. 1) пусть , мы разложили в непрерывную дробь, остаётся вопрос о сходимости, т.е
1) пусть 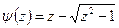 , мы разложили
, мы разложили 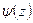 в непрерывную дробь, остаётся вопрос о сходимости, т.е.
в непрерывную дробь, остаётся вопрос о сходимости, т.е.  (сходимость будет следовать из того, что
(сходимость будет следовать из того, что 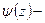 функция Марковского типа). Доказать, что
функция Марковского типа). Доказать, что 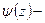 функция Марковского типа.
функция Марковского типа.
2) Рассмотрим 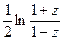 Разложить функцию в непрерывную дробь и доказать сходимость дроби.
Разложить функцию в непрерывную дробь и доказать сходимость дроби.
3) -\\- для 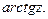
4) -\\- для 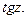
Решения. 1) Проведём 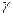 - любую простейшую жорданову спрямляемую кривую, т.ч.
- любую простейшую жорданову спрямляемую кривую, т.ч.  лежит вне.
лежит вне.
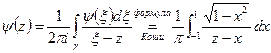 . Теперь стягиваем контур к отрезку: граничное значение функции на верхнем берегу отрезка. Здесь мнимая часть, т.е. вещественной – нет, «-2» сократилась.
. Теперь стягиваем контур к отрезку: граничное значение функции на верхнем берегу отрезка. Здесь мнимая часть, т.е. вещественной – нет, «-2» сократилась. 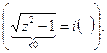
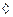
2) 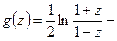 голоморфна в окрестности точки
голоморфна в окрестности точки 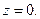 А теорема Маркова для функции в точке
А теорема Маркова для функции в точке 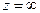
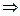 сделаем замену переменной
сделаем замену переменной  голоморфна в окрестности точки
голоморфна в окрестности точки 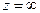 . Докажем, что
. Докажем, что 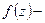 функция Марковского типа. Напишем ряд Лорана в окрестности точки
функция Марковского типа. Напишем ряд Лорана в окрестности точки 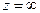 .
. 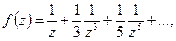 таким образом,
таким образом, 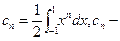 коэффициент при
коэффициент при 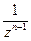 , если n – чётное, то
, если n – чётное, то 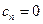 , если n – нечётное, то
, если n – нечётное, то 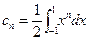 , тогда это и есть мера
, тогда это и есть мера 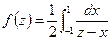 . Для функции
. Для функции 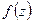 сходимость дроби вне отрезка
сходимость дроби вне отрезка 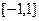 . А для
. А для 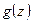 в единичном круге .
в единичном круге . 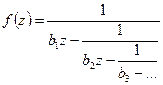 ,
, 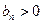 Дроби такого вида называются Р-дробями. Тогда
Дроби такого вида называются Р-дробями. Тогда 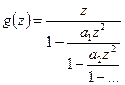 (другая нормировка и замена). Дроби такого вида называются С-дробями. Как посчитать эти коэффициенты?
(другая нормировка и замена). Дроби такого вида называются С-дробями. Как посчитать эти коэффициенты? 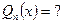
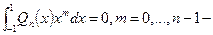 многочлены Лежандра. Для них справедлива формула Родрига:
многочлены Лежандра. Для них справедлива формула Родрига: 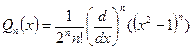 - стандартная нормировка
- стандартная нормировка 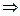 получим коэффициенты рекуррентных соотношений
получим коэффициенты рекуррентных соотношений 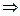 коэффициенты. Подставляем в интегральную формулу и интегрируем по частям (её легко проверить). Теперь: Посчитаем:
коэффициенты. Подставляем в интегральную формулу и интегрируем по частям (её легко проверить). Теперь: Посчитаем: 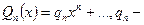 старший коэффициент многочлена, и число
старший коэффициент многочлена, и число 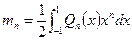 ,
, 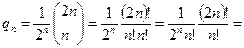 в 2n! – уничтожается чётная часть.
в 2n! – уничтожается чётная часть. 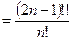 .
.
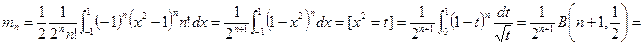
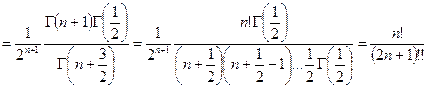 А тогда само рекуррентное соотношение имеет вид: Мы знаем, что
А тогда само рекуррентное соотношение имеет вид: Мы знаем, что  , из уравнения старших коэффициентов:
, из уравнения старших коэффициентов: 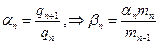 см. доказательство этой
см. доказательство этой 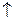 формулы.
формулы. 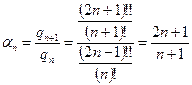
|
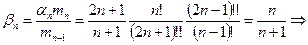 числа а и в – произведение
числа а и в – произведение 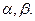
3) 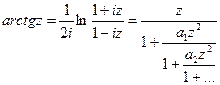 сходимость будет в плоскости с вертикальными разрезоми:
сходимость будет в плоскости с вертикальными разрезоми:
(замена переменной).
4)  Рассмотрим степенные ряды вида:
Рассмотрим степенные ряды вида: 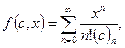 где
где 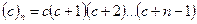 - символ Похгоммера,
- символ Похгоммера, 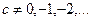
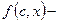 вырожденные параметрические функции,
вырожденные параметрические функции, 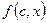 сходится,
сходится, 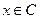 . Докажем тождество:
. Докажем тождество: 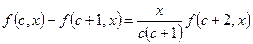 Проверим его: При
Проверим его: При 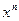 - коэффициенты слева и справа: Левая часть:
- коэффициенты слева и справа: Левая часть: 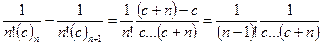 А справа:
А справа: 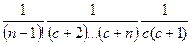 они равны.
они равны. 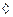 Напишем непрерывную дробь:
Напишем непрерывную дробь: 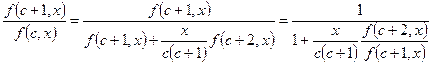 тогда можно применить метод индукции
тогда можно применить метод индукции 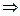 непрерывная дробь, итак,
непрерывная дробь, итак, 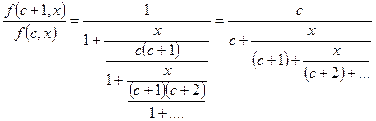 - это непрерывная дробь Ламберта.
- это непрерывная дробь Ламберта.
Подставим 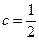 , тогда:
, тогда: 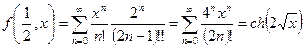
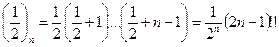
 (аналогично), тогда если сделать замену переменной:
(аналогично), тогда если сделать замену переменной: 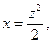 то получим:
то получим:  , а у обычного
, а у обычного 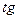 «-», т.к.
«-», т.к. 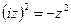 Сходимость следует из теоремы.
Сходимость следует из теоремы.
Теорема (Эйлера): 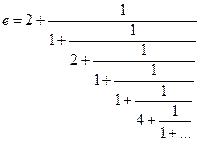 (начало: 1, 1, 2n ).
(начало: 1, 1, 2n ).
Дата добавления: 2015-09-02; просмотров: 539;