Теорема Гаусса-Маркова. В классическом множественном регрессионном анализе обычно делаются следующие предпосылки:

В классическом множественном регрессионном анализе обычно делаются следующие предпосылки:

1. Математическое ожидание случайного члена 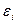равно нулю в любом наблюдении

(15.14)

2. Дисперсия случайного члена 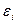постоянна для всех наблюдений

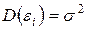. (15.15)

3. Значения случайного члена в любых наблюдениях 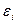и 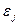не коррелируют между собой

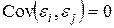
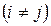. (15.16)

Это условие с учетом того, что 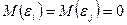принимает вид

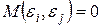
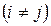(15.17)

4. Случайный член должен быть распределен независимо от объясняющих переменных xi в одних и тех же наблюдениях

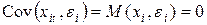(15.18)

Следует сказать, что последнее условие заведомо выполняется, если объясняющие переменные 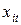считаются детерминированными величинами.

5. Матрица является неособенной, т. е. столбцы матрицы X линейно независимы.

6. Значения случайного члена 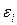распределены по нормальному закону.

Определение 15.1. Модель (15.1), удовлетворяющая приведенным предпосылкам 1-6, называется классической нормальной линейной моделью множественной регрессии.

Определение 15.2. Модель (15.1), удовлетворяющая приведенным предпосылкам 1-5, называется классической линейной моделью множественной регрессии.

Согласно теореме Гаусса-Маркова, при выполнении указанных предпосылок оценки параметров линейной множественной регрессии, полученные методом наименьших квадратов, будут несмещенными и эффективными (т. е. будут иметь наименьшую дисперсию) в классе линейных несмещенных оценок.

Нарушение одного из условий Гаусса-Маркова приводит к нарушению эффективности оценок, т. е. в классе несмещенных оценок можно найти такие, которые имеют меньшую дисперсию. После построения модели необходимо вычислить значения остатков 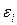и проверить выполнение предпосылок 1-6, так как их нарушение снижает качество модели. Если условия нарушаются, то следует модернизировать модель соответствующим образом. Эти вопросы будут рассмотрены далее.

После построения модели необходимо вычислить значения остатков 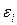и проверить выполнение предпосылок 1-6, так как их нарушение снижает качество модели. Если условия нарушаются, то следует модернизировать модель соответствующим образом.