Оценка параметров уравнения линейной множественной регрессии

Рассмотрим уравнение линейной множественной регрессии

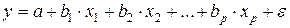. (15.1)

Для оценки параметров уравнения множественной регрессии обычно применяется метод наименьших квадратов (МНК), согласно которому следует выбирать такие значения параметров а и 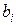, при которых сумма квадратов отклонений фактических значений результативного признака 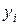от теоретических значений 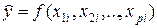(при тех же значениях фактора ) минимальна, т. е.

.

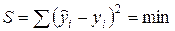С учетом (15.1), величина S является функцией неизвестных параметров а и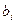

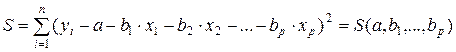(15.2)

Оптимальные значения параметров а и 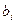удовлетворяют условиям

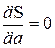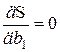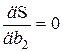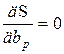, , , … (15.3)

Выполняя соответствующие вычисления, получим для определения параметров а и 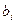следующую систему уравнений

,

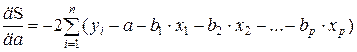, (15.4)

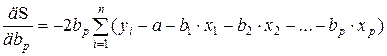
откуда после некоторых преобразований получается система нормальных уравнений метода наименьших квадратов

;

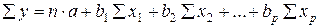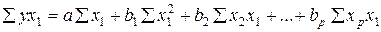(15.5)

……………………………………………

.

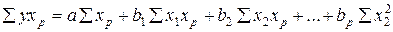Решение системы (15.5) удобно записать с помощью матричных обозначений. Обозначим

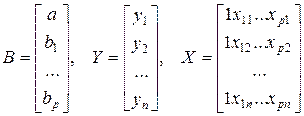, (15.6)

где B - матрица-столбец (p+1×1) из коэффициентов а и ;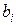

Y - матриц-столбец (n×1) исходных значений зависимой переменной y;

X - матрица (p+1×n) исходных значений независимых переменных 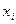, в которой первый столбец из единиц можно рассматривать как значения «фиктивной» переменной, соответствующей коэффициенту а.

В этих обозначениях система (15.5) примет вид

(15.7)

где 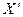- транспонированная матрица X. Матрица является неособенной квадратной размерности (p+1×p+1) при условии, что столбцы матрицы X линейно независимы.

Решение системы (15.7) определяется соотношением

. (15.8)

Независимые переменные 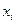имеют различный экономический смысл, разные единицы измерения и масштаб. Если нужно определить степень относительного влияния отдельных факторов x_i на изменение результативной переменной y, то переменные 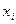следует привести к сопоставимому виду. Это можно осуществить, вводя, так называемые, «стандартизованные» переменные 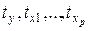с помощью соотношений

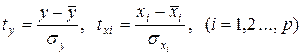(15.9)

где 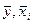- средние значения, 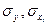- средние квадратические отклонения переменных y и .

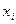Стандартизованные переменные обладают следующими свойствами: 1). средние значения равны нулю );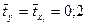

2).средние квадратические отклонения равны единице .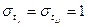

Уравнения множественной регрессии в стандартизованных переменных принимает вид

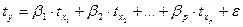. (15.10)

Величины 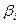называются стандартизованными коэффициентами. Их связь коэффициентами множественной регрессии 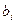задается соотношениями

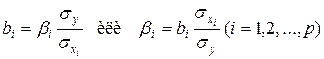. (15.11)

Параметр а уравнения (15.1) можно определить из соотношения

. (15.12)

Стандартизованные коэффициенты регрессии 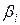показывают, на сколько сигм (средних квадратических отклонений) изменится в среднем результативный признак y за счет изменения соответствующего фактора на одну сигму при неизмененном значении других факторов, закрепленных на среднем уровне.

Система нормальных уравнений МНК (15.5) в стандартизованных переменных принимает вид:

;

;

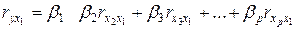…………………………………….. (15.13)

.

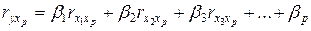Стандартизованные коэффициенты регрессии сравнимы между собой, что позволяет ранжировать факторы по силе их воздействия на результат. Большее относительное влияние на изменение результативной переменной y оказывает тот фактор, которому соответствует большее по модулю значение коэффициента .

Отметим, что в случае парной линейной регрессии стандартизованный коэффициент регрессии β совпадает с линейным коэффициентом корреляции . Для оценки параметров нелинейных уравнений множественной регрессии предварительно осуществляется преобразование последних в линейную форму (с помощью замены переменных) и МНК применяется для нахождения параметров линейного уравнения множественной регрессии в преобразованных переменных.

В случае внутренне нелинейных зависимостей (которые невозможно привести к линейному виду) для оценки параметров по методу наименьших квадратов приходится применять методы нелинейной оптимизации.