Выбор формы уравнения регрессии
Различают следующие виды уравнений множественной регрессии: линейные, нелинейные, сводящиеся к линейным, и нелинейные, не сводящиеся к линейным (внутренне нелинейные). В первых двух случаях для оценки параметров модели применяются классического линейного регрессионного анализа. В случае внутренне нелинейных уравнений для оценки параметров приходится применять методы нелинейной оптимизации.
Основное требование, предъявляемое к уравнениям регрессии, заключается в наличии наглядной экономической интерпретации модели и ее параметров.
Исходя из этих соображений, наиболее часто используются линейная и степенная зависимости.
Линейная множественная регрессия имеет вид
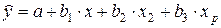 (14.4)
(14.4)
Параметры 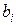 при факторах
при факторах 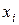 называются коэффициентами «чистой» регрессии. Они показывают, на сколько единиц в среднем изменится результативный признак y за счет изменения соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.
называются коэффициентами «чистой» регрессии. Они показывают, на сколько единиц в среднем изменится результативный признак y за счет изменения соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.
Предположим, например, что зависимость спроса на товар ( 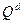 ) от цены (P) и дохода (I) характеризуется следующим уравнением:
) от цены (P) и дохода (I) характеризуется следующим уравнением:
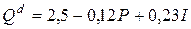 .
.
Коэффициенты данного уравнения говорят о том, что при увеличении цены на единицу, спрос уменьшится в среднем на 0,12 единиц измерения спроса, а при увеличении дохода на единицу, спрос возрастет в среднем 0,23 единицы.
Параметр а в (14.4) не всегда может быть содержательно проинтерпретирован.
Степенная множественная регрессия имеет вид
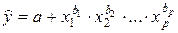 (14.5)
(14.5)
Параметры 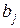 (степени факторов
(степени факторов 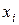 ) являются коэффициентами эластичности. Они показывают, на сколько процентов в среднем изменится результативный признак y за счет изменения соответствующего фактора
) являются коэффициентами эластичности. Они показывают, на сколько процентов в среднем изменится результативный признак y за счет изменения соответствующего фактора 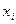 на 1 % при неизмененном значении остальных факторов.
на 1 % при неизмененном значении остальных факторов.
Наиболее широкое применение этот вид уравнения регрессии получил в производственных функциях, а также при исследовании спроса и потребления.
Например, зависимость выпуска продукции Y от затрат капитала K и труда L:
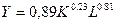
говорит о том, что увеличение затрат капитала K на 1 % при неизменных затратах труда вызывает увеличение выпуска продукции Y на 0,23 %. Увеличение затрат труда L на 1 % при неизменных затратах капитала K вызывает увеличение выпуска продукции Y на 0,81 %.
Экономический смысл имеет также сумма коэффициентов 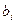 каждого фактора (сумма эластичностей)
каждого фактора (сумма эластичностей) 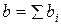 . Эта величина дает обобщенную характеристику эластичности производства.
. Эта величина дает обобщенную характеристику эластичности производства.
Если значение b > 1, то говорят, что функция имеет возрастающий эффект от масштаба производства. Значение b = 1 говорит о постоянном масштабе производства. Если значение b < 1, то имеет место убывающий эффект от масштаба производства.
Если один и тот же фактор вводится в регрессию в разных степенях, то каждая степень рассматривается как самостоятельный фактор. Например, если в нелинейной модели с двумя факторами 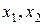 .
.
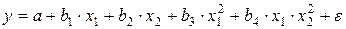 ,
,
величины 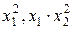 рассматривать как новые дополнительные факторы, то, используя замену переменных
рассматривать как новые дополнительные факторы, то, используя замену переменных 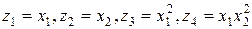 , ее можно привести к линейному уравнению регрессии с четырьмя факторами:
, ее можно привести к линейному уравнению регрессии с четырьмя факторами:
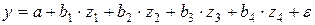 .
.
Дата добавления: 2015-11-06; просмотров: 1676;
