Понятие мультиколлинеарности, ее влияние на оценки параметров модели.
Оценка параметров множественной регрессии. Свойства коэффициентов множественной регрессии.
Понятие мультиколлинеарности, ее влияние на оценки параметров модели.
Определение 14.1. Множественной регрессией называют уравнение связи с несколькими независимыми переменными:
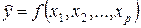 (14.1)
(14.1)
Переменная у называется зависимой, объясняемой или результативным признаком  – независимые, объясняющие переменные или факторные признаки (факторы).
– независимые, объясняющие переменные или факторные признаки (факторы).
Соответствующая регрессионная модель имеет вид
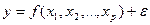 (14.2)
(14.2)
где  - ошибка модели, являющаяся случайной величиной.
- ошибка модели, являющаяся случайной величиной.
Множественная регрессия применяется в ситуациях, когда из множества факторов, влияющих на результативный признак, нельзя выделить один доминирующий фактор и необходимо учитывать влияние нескольких факторов. Например, объем выпуска продукции определяется величиной основных и оборотных средств, численностью персонала, уровнем менеджмента и т. д., уровень спроса зависит не только от цены, но и от имеющихся у населения денежных средств.
Основная цель множественной регрессии – построить модель с несколькими факторами и определить при этом влияние каждого фактора в отдельности, а также их совместное воздействие на изучаемый показатель.
Постановка задачи множественной регрессии: по имеющимся данным n наблюдений (табл. 3.1) за совместным изменением p+1 параметра y и 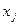 и
и 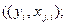
 необходимо определить аналитическую зависимость
необходимо определить аналитическую зависимость 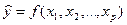 , наилучшим образом описывающую данные наблюдений.
, наилучшим образом описывающую данные наблюдений.
Таблица 14.1
Результаты наблюдений
| y | 
| 
| … | 
| |
| 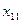
| 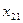
| … | 
| |
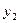
| 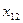
| 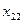
| … | 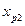
| |
| … | … | … | … | … | … |
| n | 
| 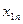
| 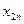
| … | 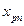
|
Каждая строка таблицы содержит p +1 число и представляет собой результат одного наблюдения. Наблюдения различаются условиями их проведения.
Вопрос о том, какую зависимость следует считать наилучшей, решается на основе какого-либо критерия. В качестве такого критерия обычно используется минимум суммы квадратов отклонений расчетных или модельных значений результативного показателя 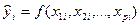 от наблюдаемых значений
от наблюдаемых значений 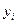
 .
.
Как и в случае парной регрессии, построение уравнения множественной регрессии предполагает решение двух задач (или, другими словами, осуществляется в два этапа):
1) спецификация модели;
2) оценка параметров выбранной модели.
В свою очередь, спецификация модели включает в себя решение двух задач:
– отбор p факторов  , подлежащих включению в модель;
, подлежащих включению в модель;
– выбор вида аналитической зависимости 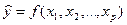 .
.
Дата добавления: 2015-11-06; просмотров: 861;
