Проверка качества уравнения регрессии. F-критерий Фишера

Как и в случае парной регрессии для оценки качества полученного множественной уравнения регрессии (15.1) можно использовать коэффициент детерминации, представляющий собой отношение объясненной части 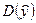дисперсии переменной у ко всей дисперсии D(y)

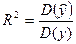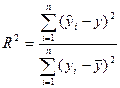или . (15.19)

где

, .

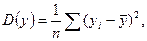
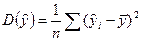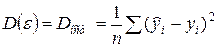Коэффициент детерминации 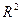принимает значения в диапазоне от нуля до единицы 0 ≤ 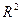≤ 1 и показывает, какая часть дисперсии результативного признака y объяснена уравнением регрессии. Чем выше значение 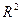, тем лучше данная модель согласуется с данными наблюдений.

Оценка статистической значимости уравнения регрессии (а также коэффициента детерминации 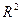) осуществляется с помощью F-критерия Фишера

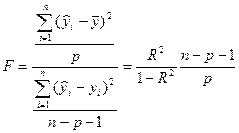, (15.20)

где p - число независимых переменных в уравнении регрессии (15.1).

Согласно F-критерию Фишера, выдвигаемая «нулевая» гипотеза 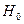о статистической незначимости уравнения регрессии отвергается при выполнении условия 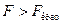, где 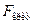определяется по таблицам F-критерия Фишера по двум степеням свободы , 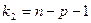и заданному уровню значимости α.

Для оценки тесноты связи факторов с исследуемым признаком, задаваемой построенным уравнением регрессии 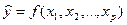, используется коэффициент множественной корреляции R

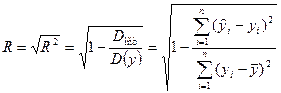. (15.21)

Коэффициент множественной корреляции R принимает значения в диапазоне 0 ≤ R ≤ 1.

Чем ближе величина R к единице, тем теснее данная связь, тем лучше зависимость 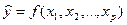согласуется с данными наблюдений. При R=1 ( 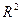= 1) связь становится функциональной, т. е. соотношение 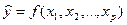точно выполняется для всех наблюдений.

Коэффициент множественной корреляции может использоваться как характеристика качества построенного уравнения регрессии 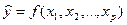, точности построенной модели.

Величина коэффициента множественной корреляции не может быть меньше максимального парного индекса корреляции .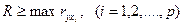

В случае линейной зависимости (3.6) коэффициент корреляции R связан с парными коэффициентами корреляции 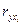соотношением

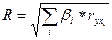, (15.22)

где – стандартизованные коэффициенты регрессии (15.1).

Использование коэффициента множественной детерминации 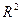для оценки качества модели, обладает тем недостатком, что включение в модель нового фактора (даже несущественного) автоматически увеличивает величину .

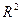Поэтому при большом количестве факторов предпочтительнее использовать, так называемый, скорректированный, улучшенный (adjusted) коэффициент множественной детерминации 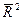, определяемый соотношением

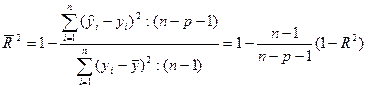, (15.23)

где p – число факторов в уравнении регрессии, n – число наблюдений

Чем больше величина p, тем сильнее различия 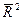и .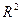

При использовании 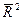для оценки целесообразности включения фактора в уравнение регрессии следует однако учитывать, что увеличение 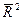при включении нового фактора не обязательно свидетельствует о его значимости, так как значение увеличивается 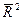всегда, когда t-статистика больше единицы ( ).

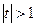При заданном объеме наблюдений и при прочих равных условиях с увеличением числа независимых переменных (параметров) скорректированный коэффициент множественной детерминации убывает. При небольшом числе наблюдений скорректированная величина коэффициента множественной детерминации 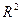имеет тенденцию переоценивать долю вариации результативного признака, связанную с влиянием факторов, включенных в регрессионную модель.

Отметим, что низкое значение коэффициента множественной корреляции и коэффициента множественной детерминации 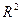может быть обусловлено следующими причинами:

– в регрессионную модель не включены существенные факторы;

– неверно выбрана форма аналитической зависимости, не отражающая реальные соотношения между переменными, включенными в модель.