Мультиколлинеарность
Под мультиколлинеарностью понимается высокая взаимная коррелированность объясняющих переменных.
Следствием мультиколлинеарности является линейная зависимость между столбцами наблюдений 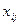 в таблице 14.1 или между столбцами матрицы X . В результате, матрица
в таблице 14.1 или между столбцами матрицы X . В результате, матрица 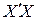 становится плохо обусловленной, что приводит к неустойчивости оценок коэффициентов регрессии, когда незначительные изменения данных наблюдений приводят к значительным изменениям оценок.
становится плохо обусловленной, что приводит к неустойчивости оценок коэффициентов регрессии, когда незначительные изменения данных наблюдений приводят к значительным изменениям оценок.
Проверка наличия мультиколлинеарности основывается на анализе матрицы парных корреляций между факторами
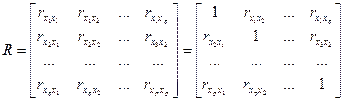 (14.3)
(14.3)
Коэффициенты парной корреляции  между объясняющими переменными используются для выявления дублирующих факторов. Линейная зависимость между объясняющими переменными
между объясняющими переменными используются для выявления дублирующих факторов. Линейная зависимость между объясняющими переменными 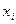 и
и  считается установленной, если выполняется условие
считается установленной, если выполняется условие 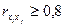 , а сами факторы называются явно коллинеарными (эмпирическое правило). Один из факторов должен быть исключен из модели. Предпочтение при этом отдается тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами.
, а сами факторы называются явно коллинеарными (эмпирическое правило). Один из факторов должен быть исключен из модели. Предпочтение при этом отдается тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами.
Наряду с парной коллинеарностью может иметь место линейная зависимость между боле, чем двумя переменными. Для оценки мультиколлинеарности факторов в этом случае может использоваться величину определителя 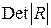 матрицы парных коэффициентов корреляции
матрицы парных коэффициентов корреляции  между факторами либо ее минимального собственного значения.
между факторами либо ее минимального собственного значения.
Чем ближе к нулю определитель (минимальное собственное значение) матрицы межфакторной корреляции, тем сильнее мультиколлинеарность между факторами и тем ненадежнее результаты множественной регрессии.
Для оценки статистической значимости мультиколлинеарности факторов может быть использован тот факт, что величина 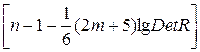 имеет приближенное распределение
имеет приближенное распределение 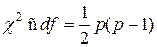 степенями свободы.
степенями свободы.
Выдвигается гипотеза 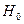 о независимости переменных, т. е.
о независимости переменных, т. е. 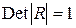 . Если фактическое значение
. Если фактическое значение  превосходит табличное (критическое)
превосходит табличное (критическое) 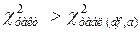 , то гипотеза
, то гипотеза 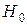 отклоняется и мультиколлинеарность считается доказанной. Для выявления мультиколлинеарности факторов можно использовать коэффициенты множественной детерминации
отклоняется и мультиколлинеарность считается доказанной. Для выявления мультиколлинеарности факторов можно использовать коэффициенты множественной детерминации 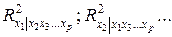 , полученные по уравнениям регрессии, в которых качестве зависимой переменной рассматривается один из факторов. Чем ближе значение коэффициента детерминации к единице, тем сильнее проявляется мультиколлинеарность факторов. Согласно эмпирическому правилу, при значении коэффициента множественной детерминации
, полученные по уравнениям регрессии, в которых качестве зависимой переменной рассматривается один из факторов. Чем ближе значение коэффициента детерминации к единице, тем сильнее проявляется мультиколлинеарность факторов. Согласно эмпирическому правилу, при значении коэффициента множественной детерминации 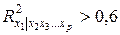 мультиколлинеарность факторов считается установленной. Оставляя в уравнении регрессии факторы с минимальной величиной коэффициента множественной детерминации, можно исключить мультиколлинеарность факторов.
мультиколлинеарность факторов считается установленной. Оставляя в уравнении регрессии факторы с минимальной величиной коэффициента множественной детерминации, можно исключить мультиколлинеарность факторов.
Для преодоления явления линейной зависимости между факторами используются такие способы, как:
- исключение одного из коррелирующих факторов;
- переход с помощью линейного преобразования к новым некоррелирующим независимым переменным. Например, переход к главным компонентам вектора исходных объясняющих переменных (что позволяет также уменьшить количество рассматриваемых факторов), переход к последовательным разностям во временных рядах  и т. п.;
и т. п.;
- переход к смещенным оценкам, имеющим меньшую дисперсию. В частности, при использовании «ридж-регрессии» применяются смещенные оценки вектора параметров  , где
, где 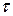 - некоторое положительной число,
- некоторое положительной число,  единичная матрица порядка p+1. Такое преобразование увеличивает определитель матрицы системы нормальных уравнений и повышает устойчивость результатов (снижает дисперсию оценок, которые становятся смещенными).
единичная матрица порядка p+1. Такое преобразование увеличивает определитель матрицы системы нормальных уравнений и повышает устойчивость результатов (снижает дисперсию оценок, которые становятся смещенными).
Следует также учитывать ограничение, накладываемое на количество факторов, имеющимся числом наблюдений. Количество наблюдений должно превышать количество факторов более чем в 6-7 раз.
Дата добавления: 2015-11-06; просмотров: 1731;
