Интегральная теорема Коши для односвязной области.

Теорема1. Если: 1) D – односвязная область

2) 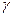- замкнутая и спрямляемая кривая, лежащая в области D.

3) f(z) – голоморфная функция в D. Тогда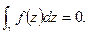

Доказательство(НЕ ПРАВИЛЬНОЕ). 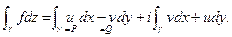По теореме Грина 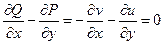в силу 2ого условия Коши-Римана. 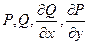- непрерывны в D для условия теоремы Грина, а мы не знаем на самом деле того, что они непрерывны J, так доказывать теорему нельзя…

Доказательство(ПРАВИЛЬНОЕ).

Замечание. 1) Теорему достаточно доказать для замкнутых ломаных.

Т.к. любую кривую можно приближать ломаной сколько угодно точно (по теореме Кантора о равномерной непрерывности) и интегралы по ломаным стремятся к длине кривой.

2) Теорему достаточно доказать для многоугольника (замкнутой ломанной без самопересечений). Т.к. точка пересечения разбивает любую замкнутую на многоугольники.

3) Теорему достаточно доказать для . Т.к. в любом многоугольнике диагонали, 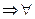многоугольник разбивается на 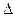-ки.

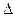Лемма (Турса). Если - замкнутый, функция f – голоморфна на 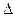, то .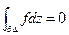

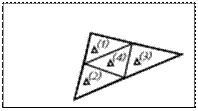
Доказательство. Обозначим: 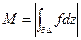проведём средние линии .

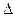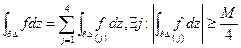. Обозначим 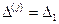. К нему применим те же рассуждения. ,

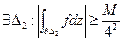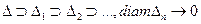. И т.д. 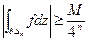т.е. оценка снизу существует.

Оценка сверху: 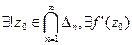по определению производной: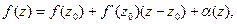 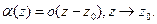Тогда 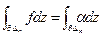(т.к. интеграл от линейной функции = 0). Оценим этот интеграл. Напишем определение о («о» малого)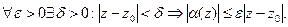

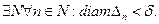
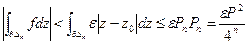(меньше диаметра, меньше периметра). Т.е. мы доказали, что 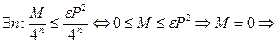лемма доказана, 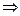теорема доказана.