Вычитая почленно из первого равенства второе, получим
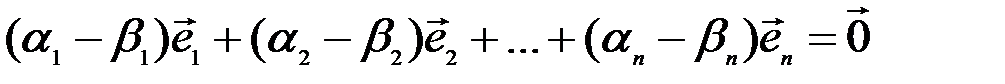 .
.
В силу линейной независимости базисных векторов 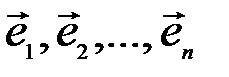 последнее равенство возможно тогда и только тогда, когда
последнее равенство возможно тогда и только тогда, когда 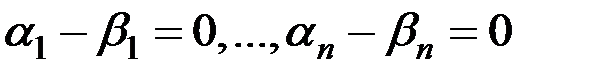 или
или 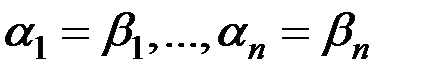 . Единственность разложения по базису доказана.
. Единственность разложения по базису доказана.
Главное значение базиса заключается в том, что операции сложения векторов и умножения их на числа при задании базиса превращаются в соответствующие операции над числами – координатами этих векторов. А именно, справедлива следующая
Теорема 3.6. При сложении двух любых векторов линейного пространства 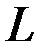 их координаты (относительно любого базиса пространства) складываются; при умножении произвольного вектора на любое число
их координаты (относительно любого базиса пространства) складываются; при умножении произвольного вектора на любое число 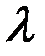 все координаты этого вектора умножаются на
все координаты этого вектора умножаются на 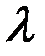 .
.
Дата добавления: 2015-09-29; просмотров: 877;
