Аксиоматическое построение теории вероятностей

Имеется большое число примеров случайных событий, для которых неприменимо классическое определение вероятности, поскольку невозможно определить конечное число элементарных событий. Следующий набор определений и аксиом предложен советским математиком А.И. Колмогоровым, эти понятия обобщают классическое определение вероятности и рассмотренные выше определения и теоремы, связанные со случайными событиями.

Пусть имеется некоторое (не обязательно конечное) множество 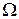. Оно называетсямножеством элементарных событий, а его элементы называютсяэлементарными событиями.

Пусть выбрано некоторое множество подмножеств F в 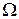. Элементы F, составленные из элементарных событий, называютсяслучайными событиями, а всё F называетсяалгеброй событий. Предполагается, что F содержит всё множество 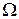(достоверное событие) и пустое множество Æ (невозможное событие). Объединение и пересечение множеств из F также принадлежит F, при этом объединение называется суммой событий, а пересечение - их произведением. Для каждого события А из F событие 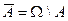(противоположное) также должно принадлежать F.

Непересекающиеся множества из F называются несовместными событиями, а непересекающиеся множества А₁, А₂, …, объединение которых дает 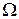, называютсяполной группой событий.

Пусть каждому событию А из F сопоставлена его мера (вероятность) P(A) такая, что выполняются следующие аксиомы.

Аксиома 1. Вероятность любого события 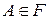неотрицательна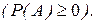

Аксиома 2. .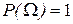

Аксиома 3. Для любых несовместных событий А₁, А₂, … из F выполняется соотношение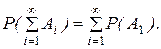

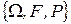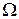ОпределениеВероятностным пространством называется тройка где - пространство элементарных событий, F – алгебра событий, Р – вероятностная мера событий из F.

Пример.Пусть 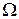состоит из конечного числа n элементарных событий, т.е. 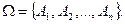Возьмем в качестве F множество всех подмножеств в 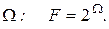Определим вероятность P(A_i) = 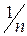для всех значений i 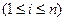. В этом случае при выполнении аксиом 1,2,3 мы получим классическое определение вероятности для любого события А из F.

Из аксиоматического построения теории вероятностей можно получить все доказанные нами формулы и теоремы. В частности, условной вероятностью P(A/B) для 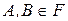называется число 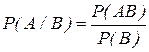, и теорема умножения вероятностей непосредственно следует из данного определения.