Функция распределения вероятностей случайной величины

Для некоторых случайных величин невозможно выделить их отдельные изолированные значения, поскольку их возможные значения заполняют некоторые промежутки. Например, мощность пласта, соответствующая определенной точке на поверхности Земли. Для описания подобных случайных величин ранее рассмотренные законы распределения вероятностей не применимы.

Пусть Х – случайная величина, а x– любое действительное число. Функцией распределения вероятностивеличины Х называется функция действительного переменного у=F(х) равная вероятности того, что Х примет значение меньше x, т.е.

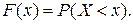
Геометрически эта вероятность равна вероятности попадания значения х в промежуток 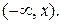См. рис. 1.

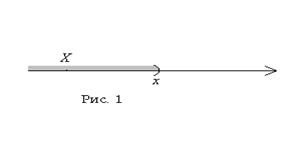Для любой дискретной величины Х функция y=F(x) кусочно постоянна и имеет разрывы во всех точках возможных значений x_k величины Х.

Отметим следующие свойства функции распределения вероятностей случайной величины Х.

Свойство 1.Функция F(x) определена на всей числовой оси и принимает свои значения из промежутка [0,1]: 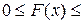1.

Свойство 2.Если 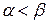любые числа, то вероятность того, что значение Х попадет в промежуток 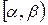, равна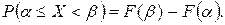

Свойство 3.Функция 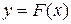не убывает для всех х.

Свойство 4.Для любой случайной величины Хверно:

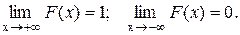
В частности, если все возможные значения Х принадлежит отрезку [a,b], то 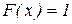при x>b 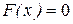и при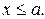

Случайная величина Х, функция распределения 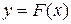которой непрерывно дифференцируема для всех x, называется непрерывной случайной величиной.

Теорема 1.Вероятность того, что непрерывная величина Х примет любое фиксированное значение x равна нулю: .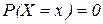

Это свойство показывает существенное различие между дискретными и непрерывными величинами, из него следует, что дискретная величина не является непрерывной.

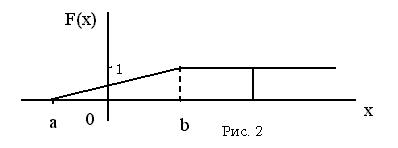На следующем рисунке изображен график функции распределения непрерывной случайной величины определенной в отрезке [a,b].(см. рис. 2).

6.2. Плотность распределения вероятностей непрерывной случайной величины

Следующая характеристика непрерывной величины более наглядна по сравнению с функцией распределения вероятности.

Плотностью(распределения вероятностей) непрерывной случайной величины Х называется производная ее функции распределения: .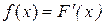

Перечислим основные свойства плотности непрерывной величины.

Свойство 1.Плотность случайной величины Х неотрицательна:

.

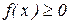Свойство 2. Для любого отрезка 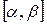вероятность попадания значения величины 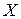в этот отрезок равна интегралу от плотности 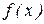случайной величины по этому отрезку:

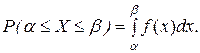
Свойство 3.Для непрерывной величины 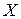с плотностью 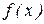верно равенство .

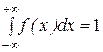Свойство 4 (формула обращения). Если 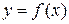- плотность непрерывной величины 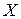, то ее функция распределения вероятностей равна

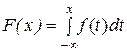
6.3. Математическое ожидание и дисперсия непрерывной величины

Пусть все возможные значения непрерывной случайной величины X принадлежат отрезку 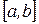. Разобьем его n частей точками 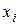и заменим приближенно все значения величины из промежутк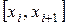а на 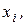вероятность величине попасть в этот промежуток приближенно равна 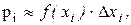где 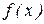– плотность величины 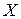. В результате величина 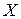превратится в дискретную и, используя определение математического ожидания дискретной величины, получим, что 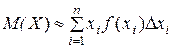.Перейдя в этом соотношении к пределу при максимальном 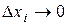стремящемся к нулю, получим обоснование для следующего определения.

Математическим ожиданием непрерывной случайной величины Х с плотностью 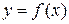называется число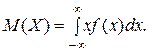

В частности, если все значения 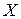лежат в отрезке 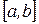, то

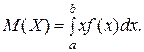
Здесь и в дальнейшем будем предполагать, что все указанные несобственные интегралы сходятся абсолютно. Аналогично определяется

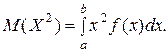
Следующее определение дисперсии повторяет ее определение для дискретного случая. Дисперсией непрерывной случайной величины с плотностью распределения 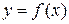называется число

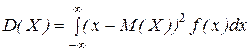
(или, равносильно, .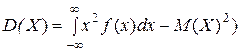

Эти понятия обладают всеми свойствами математического ожидания и дисперсии, которые были отмечены выше для дискретных величин.

Выводы. По данной теме нами были рассмотрены, функция распределения вероятностей и ее свойства, непрерывные случайные величины, плотность распределения вероятностей и ее свойства, математическое ожидание и дисперсия непрерывной случайной величины.

Лекции№13-14. Равномерная, показательная и нормальная случайные величины.

План. Основные примеры непрерывных случайных величин. Равномерная, показательная и нормальная случайные величины и их свойства..

В следующих пунктах мы рассмотрим основные примеры непрерывных случайных величин.

6.4. Равномерно распределенная случайная величина

Равномерно распределенной в отрезке 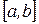случайной величиной 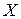называется величина, плотность которой 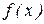постоянна в этом отрезке, а вне его :

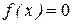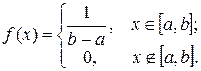
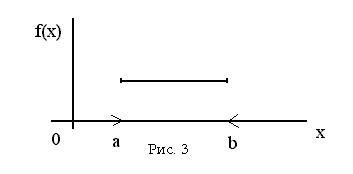График плотности 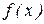равномерно распределенной величины приведен на рис 3.

Математическое ожидание этой величины совпадает с серединой отрезка : .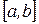

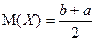Дисперсия равномерной величины равна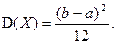

СКО равномерной величины составляет примерно 0,289 длины отрезка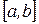

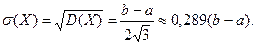
Примерами равномерных величин являются всевозможные ошибки и погрешности округления. Например, если цифровой индикатор часов выдает только целое число часов и минут (секунды отбрасываются), то ошибка округления Х такого индикатора есть равномерно распределенная в отрезке 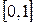величина. Средняя ошибка такого индикатора составляет 0,5 мин, а СКО этой ошибки–0,289 мин.

6.5. Показательная случайная величина

Показательной случайной величиной с параметром 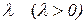называется случайная величина имеющая плотность вида

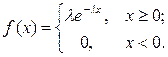
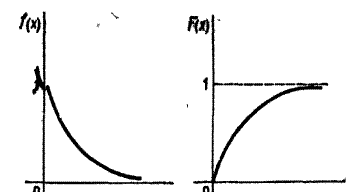Графики этой плотности и функции распределения вероятностей приведены на рис 4.

Несложно проверить, что 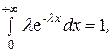т.е. что определение данной плотности корректно.

Математическое ожидание этой величины находится с помощью интегрирования по частям:

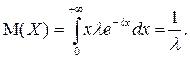
Рис. 4.

Аналогично находится 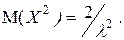Следовательно, 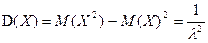и .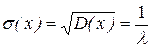

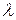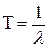Показательные случайные величины используется в теории массового обслуживания. Так, время ожидания очередной заявки, поступающей на пункт обслуживания (телефонный звонок, приход клиента и т. д. ) есть показательная величина с параметром , где – среднее время между двумя заявками.

В теории надежности время работы изделия до отказа часто является показательной величиной, где 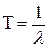– среднее время работы такого изделия до отказа.

Пример. Пусть среднее время безотказной работы некоторого прибора составляет 4 года, а срок гарантийного ремонта определен в 1 год. Найдем вероятность того, что приобретенный прибор потребует гарантийного ремонта.

Время безотказной работы прибора - Х есть показательная величина с параметром 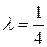. С помощью свойства 2 плотности найдем вероятность того, что 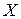не превосходит одного года.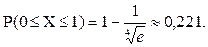

6.6. Нормальная случайная величина.

Определение. Нормальной случайной величиной с параметрами а и 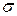называется случайная величина, плотность которой есть

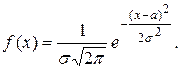
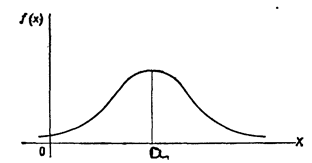Схематичный вид графика этой плотности изображен на рис 5.

Эта кривая называется Гауссовской (нормальной) кривой. При 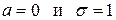нормальная случайная величина называется нормированной, ее плотность совпадает с функцией:

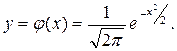
Рис. 5.

Отметим основные свойства плотности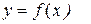

1) Эта функция положительна, возрастает на промежутке 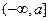и убывает на промежутке 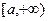. В точке 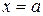функция достигает своего наибольшего значения .

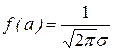2) График функции симметричен относительно прямой .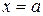

3) Точки 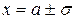являются точками перегиба функции.

4) .

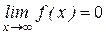5) 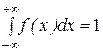, что означает корректность этого определения плотности.

Найдем математическое ожидание и дисперсию нормальной случайной величины.

,

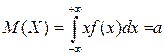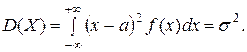
Следовательно, СКО 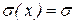. Итак, нормальная случайная величина определяется двумя параметрами математическим ожиданием 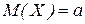и СКО .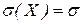

Теорема 2.Вероятность попадания значения нормальной величины с параметрами а и 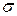в промежуток 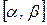равна

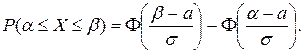
Несмотря на кажущуюся громоздкость функции плотности нормальной величины, эта величина одна из самых часто встречающихся в приложениях теории вероятностей. Ее распространенность объяснятся следующей теоремой А.М. Ляпунова.

Центральная предельная теорема Ляпунова (понятие о теореме) Пусть случайная величина Х есть сумма большого числа слабо зависящих величин, каждая из которых мало влияет на Х, тогда Х приближению является нормальной величиной.

Согласно теореме Ляпунова всевозможные погрешности, связанные с измерением различных величин, изготовлением изделий можно приближенно считать нормальными величинами, поскольку они складываются из очень большого числа незначительных случайных факторов.

Выводы. По данной теме нами были рассмотрены основные примеры непрерывных случайных величин: равномерная, показательная, нормальная случайные величины и их свойства.Центральная предельная теорема Ляпунова.