Схема Бернулли
Пусть производится n испытаний; в каждом i-ом испытании одно из независимых событий 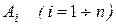 может наступить с постоянной отличной от нуля и единицы вероятностью p. Такую ситуацию будем называтьсхемой Бернуллис параметрами n и p. Пусть
может наступить с постоянной отличной от нуля и единицы вероятностью p. Такую ситуацию будем называтьсхемой Бернуллис параметрами n и p. Пусть 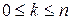 . Обозначим через
. Обозначим через 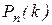 вероятность того, что в указанной схеме Бернулли события Аi появятся ровно k раз.
вероятность того, что в указанной схеме Бернулли события Аi появятся ровно k раз.
Теорема 1.Для схемы Бернулли с параметрами n, p
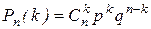 .
.
Здесь q=1–p - есть вероятность противоположенных к Ai событий.
Эта формула называется формулой Бернулли.
Пример. Найдем вероятность того, что в трех из данных пяти скважин будут обнаружены песчаные пробки, если вероятность обнаружения такой пробки в каждой скважине равна 0,5. Эта ситуация относится к схеме Бернулли с параметрами n = 5 и p = 0,5. Для k = 3 получим
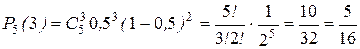 .
.
4.2. Функция 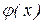 . Локальная теорема Муавра-Лапласа
. Локальная теорема Муавра-Лапласа
Хотя формула Бернулли позволяет точно находить вероятности 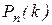 , при большом количестве испытаний n она мало применима вследствие вычислительных трудностей. Для больших n имеется несколько приближенных формул, в которых используются специальные функции, для них в теории вероятностей сохраняются постоянные обозначения.
, при большом количестве испытаний n она мало применима вследствие вычислительных трудностей. Для больших n имеется несколько приближенных формул, в которых используются специальные функции, для них в теории вероятностей сохраняются постоянные обозначения.
Функцией 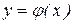 называетсяфункция
называетсяфункция 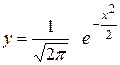 . Отметим некоторые ее свойства.
. Отметим некоторые ее свойства.
1) Эта функция определена, положительна и бесконечно дифференцируема для всех действительных x.
2) Функция 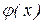 четная, т.е.
четная, т.е. 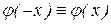 .
.
3) На промежутке 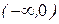 эта функция возрастает, а на промежутке
эта функция возрастает, а на промежутке 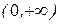 она убывает. При
она убывает. При 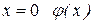 принимает свое наибольшее значение
принимает свое наибольшее значение 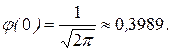
4) 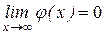 .
.
Теорема 2 (локальная теорема Муавра - Лапласa).Пусть в схеме Бернулли с параметрами n, p, числа n и 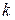 стремятся к бесконечности таким образом, что
стремятся к бесконечности таким образом, что 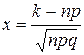 остается постоянным, тогда
остается постоянным, тогда
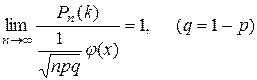 .
.
Из этой теоремы следует, что при больших n имеет место приближенное равенство
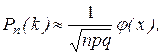
причем чем n больше, тем это равенство точнее.
Пример. Найдем вероятность того, что среди 400 изделий окажется ровно 80 бракованных, если вероятность брака для каждого изделия равна 0,2.
Здесь мы имеем дело со схемой Бернулли с параметрами n = 400, p = 0,2. Поскольку k = 80, то 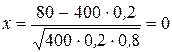 . Следовательно,
. Следовательно,
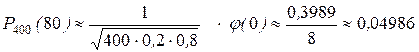 .
.
4.3. Функция Ф(x). Интегральная теорема Муавра-Лапласа
Для больших значений n в схеме Бернулли часто большее значение имеет не вероятность 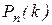 , а вероятность того, что число появлений событий – k для n испытаний будет заключено в некотором промежутке [k1,k2].
, а вероятность того, что число появлений событий – k для n испытаний будет заключено в некотором промежутке [k1,k2].
Пусть числа k1, k2 таковы, что 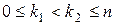 . Обозначим через Pn(k1,k2) вероятность того, что в схеме Бернулли с параметрами n, p число k наступлений событий Аi удовлетворяет неравенству
. Обозначим через Pn(k1,k2) вероятность того, что в схеме Бернулли с параметрами n, p число k наступлений событий Аi удовлетворяет неравенству 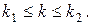 Понятно, что
Понятно, что
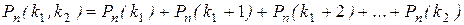
Первообразная для 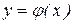 функция -
функция - 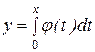 называется функцией
называется функцией 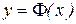 . Отметим свойства функции
. Отметим свойства функции 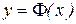 .
.
1)Функция 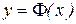 определена, бесконечно дифференцируема и является возрастающей для всех действительных x.
определена, бесконечно дифференцируема и является возрастающей для всех действительных x.
2) 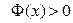 для x>0 и
для x>0 и 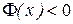 для x<0. Функция
для x<0. Функция 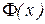 нечетна, т.е.
нечетна, т.е. 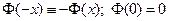 .
.
3) 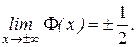
Значения функции 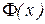 можно определять с помощью численного интегрирования или её таблицы.
можно определять с помощью численного интегрирования или её таблицы.
Теорема 3 (интегральная теорема Муавра- Лапласа). Пусть для схемы Бернулли с параметрами n, p числа n, k1 и k2 стремятся к бесконечности таким образом, что числа 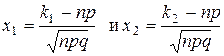 остаются постоянными, тогда
остаются постоянными, тогда 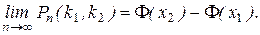
Из этой теоремы следует приближенное равенство
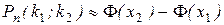 ,
,
которое тем точнее, чем больше n.
Пример. При условии предыдущего примера 400 изделиях найдем вероятность того, что число бракованных изделий в этой партии окажется не более 100. То есть, в условиях схемы Бернулли с параметрами n = 400, p = 0,2 найдем вероятность P400(0;100).
Здесь 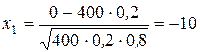 ,
, 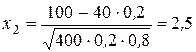 .
.
Хотя значение x1 = -10 отсутствует в таблице, значение 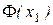 найдем используя свойства этой функции:
найдем используя свойства этой функции: 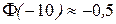 . Следовательно,
. Следовательно,
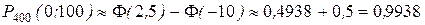 .
.
Дата добавления: 2015-10-21; просмотров: 1285;
