Закон больших чисел. Под законом больших чисел в теории вероятностей понимается набор теорем, описывающих поведение суммы большого числа случайных величин

Под законом больших чисел в теории вероятностей понимается набор теорем, описывающих поведение суммы большого числа случайных величин. При выполнении некоторых условий, эта сумма обладает свойствами практически не зависящими от свойств слагаемых (как в теореме Ляпунова), а часто эта сумма теряет свойства случайности и приближается к постоянной. Следующие теоремы одинаково справедливы как для дискретных, так и для непрерывных величин.

Теорема 1 (Неравенство Чебышева). Пусть Х – случайная величина, М( 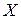) ее математическое ожидание, D( 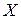) – дисперсия, 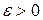-число. Тогда .

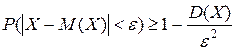Заметим, что неравенство Чебышева, оценивающее снизу вероятность отклонения значений случайной величины от ее мат. ожидания часто дает слишком грубую оценку. Основное его значение теоретическое, поскольку оно используется при доказательстве ряда теорем.

Теорема Чебышева. Пусть 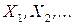- последовательность независимых случайных величин, дисперсии которых ограничены некоторым числом 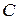, т.е. 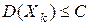для всех 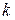. Пусть 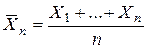- среднее арифметическое первых n этих величин, а 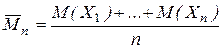среднее арифметическое их математических ожиданий. Тогда для любого 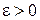верны соотношения

;

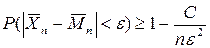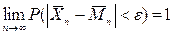
Смысл этой теоремы состоит в том, что при выполнении ее условий, вероятность отклонения среднего арифметического случайных величин от среднего арифметического их мат. ожиданий меньше чем на любое малое число 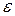с ростом n стремится к единице.

Определение. Пусть имеется последовательность случайных величин 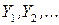. Эта последовательность называется сходящейся по вероятностик числу 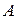если для каждого 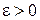верно равенство

.

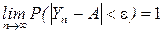Соответствующее обозначение .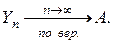

Следствие. Пусть 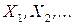последовательность независимых величин с равными мат. ожиданиями 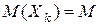и ограниченными числом С дисперсиями, тогда последовательность их средних арифметических при 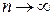сходится по вероятности к мат. ожиданию 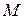, т.е.

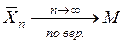
Это следствие остается верным и для одинаково распределенных случайных величин 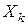, поскольку эти величины имеют равные математические ожидания и равные дисперсии.

Пусть имеется схема Бернулли с параметрами 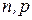, и пусть в этой серии испытаний события 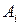наблюдались m раз. Тогда число m называется частотой, а 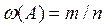называется относительной частотой, или частостью событий 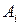. Это понятие исторически появилось раньше, чем вероятность. Из теоремы Чебышева следует следующая теорема, которая была доказана Бернулли ранее, т.е. теорема Чебышева стала обобщением теоремы Бернулли.

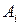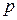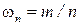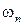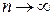Теорема Бернулли.Пусть имеется последовательность испытаний в каждом из которых события могут появляться с равными вероятностями , пусть - относительные частоты появления событий в первых n испытаниях, тогда при стремится к 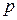по вероятности, т.е.

.

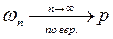Кроме того, справедливо неравенство

.

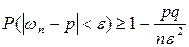.Выводы. По данной теме нами были рассмотрены неравенство Чебышева, теоремы Чебышева и Бернулли, сходимость по вероятности.