Закон распределения дискретной случайной величины. Основные примеры
Если при проведении некоторого испытания обязательно появляется заранее неопределенное число, то такое случайное явление называютслучайной величиной.Более точное определение следующее.
Определение.Случайной величиной Х называется полная группа событий, каждое из которых состоит в появлении некоторого числа. Если множество всех возможных значений случайной величины дискретно, т.е. состоит из отдельных изолированных значений, то такая величина называется дискретной случайной величиной (ДCB).
Например, Х – количество отказов некоторого оборудования на 1000 часов его работы.
Законом распределения ДСВ называется соответствие между всеми возможными значениями случайной величины и их вероятностями, т.е. таблица, в одной строке которой стоят все возможные значения этой величины, а в другой – вероятности их появления.
Так если ДСВ Х имеет возможные значения x1,x2, … которые могут приниматься с соответствующими вероятностями p1, p2, …, то ее закон распределения имеет вид
| Х | x1 | x2 | … |
| P | p1 | p2 | … |
Такая таблица может быть как конечной, так и бесконечной.
Основное свойство закона распределения состоит в том, что сумма всех вероятностей в законе распределения ДСВ всегда равна единице: 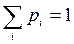 .
.
Рассмотрим теперь некоторые примеры ДСВ.
Биномиальной случайной величиной с параметрами n и p (n - натуральное, 0<p<1) называется случайная величина, принимающая целые значения 0; 1; 2; …, n с вероятностями определяемыми формулой Бернулли. Величина Х здесь равна числу появлений событий Ai в n испытаниях схемы Бернулли. Закон распределения этой биномиальной величины имеет следующий вид.
| X | … | k | … | n-1 | n | ||
| P | 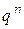
| npqn-1 | … | 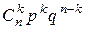
| … | npn-1q | pn |
Например, X - число бракованных изделий в некоторой партии из n изделий при вероятности брака - p для каждого изделия.
Пуассоновской случайной величиной с параметром 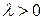 называется ДСВ, принимающая значения 0, 1, 2, … с вероятностями, определяемыми формулой Пуассона. Её закон распределения имеет вид следующей бесконечной таблицы.
называется ДСВ, принимающая значения 0, 1, 2, … с вероятностями, определяемыми формулой Пуассона. Её закон распределения имеет вид следующей бесконечной таблицы.
| X | … | 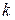
| … | ||
| P | 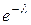
| 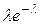
| … | 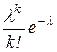
| … |
Вероятности этого закона получаются из вероятностей биномиальной величины в результате предельного перехода при 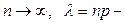 постоянная.
постоянная.
Геометрической случайной величиной с параметром 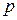 (0<p<1) называется случайная величина принимающая значения k=1, 2, … с вероятностями
(0<p<1) называется случайная величина принимающая значения k=1, 2, … с вероятностями 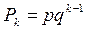 , где q=1-p. Эта величина имеет закон распределения следующего вида.
, где q=1-p. Эта величина имеет закон распределения следующего вида.
| X | … | 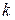
| … | |||
| P | р | pq | pq2 | … | pqk-1 | … |
Для схемы Бернулли с достаточно большим n и фиксированным p, эта величина X есть число испытаний, которые необходимо провести до первого появления события Ak.
5.2. Математическое ожидание случайной величины и его свойства
Следующее понятие позволяет охарактеризовать средневзвешенное значение ДСВ с помощью одного числа.
Определение. Математическим ожиданием ДСВ Х с законом распределения вероятностей
| Х | х1 | х2 | … |
| Р | р1 | р2 | … |
называется число, равное сумме произведений всех возможных значений X на вероятности их появления:
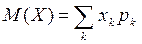 .
.
Например, если Х – дебит некоторой скважины за одни сутки, то М(Х) характеризует средний дебит этой скважины за произвольные сутки.
В случае бесконечного закона распределения здесь и в дальнейшем будем предполагать, что соответствующие ряды сходятся.
Перечислим теперь основные свойства математического ожидания.
Свойство 1.Если все возможные значения xi ДСВ Х удовлетворяют неравенству 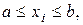 то её математическое ожидание также удовлетворяет неравенству:
то её математическое ожидание также удовлетворяет неравенству: 
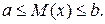
Случайная величина, принимающая одно значение с вероятностью 1, называется постоянной величиной. Эта величина обозначается таким же образом, как это значение. Её закон распределения вероятностей имеет вид
| C | С |
| Р |
Свойство 2.Математические ожидание постоянной величины равно самой этой постоянной, т.е. М(С)=С.
ПроизведениемДСВ Х на число С называется случайная величина, принимающая все значения случайной величины Х умноженные на С с теми же вероятностями, что и величина Х.
Свойство 3.Для случайной величины Х и числа С М(СХ)=СМ(Х).
Произведением (суммой)случайных величин Х и Y с законами распределения вероятностей
| Х | х1 | х2 | … | и | Y | y1 | y2 | … |
| Р | р1 | р2 | … | Р | 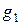
| 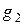
| … |
называется случайная величина, принимающая все возможные значения 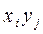 (или
(или 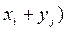 с вероятностями, равными вероятностям совместного появления соответствующих значений xi и
с вероятностями, равными вероятностям совместного появления соответствующих значений xi и 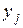 величин X и Y.
величин X и Y.
Случайные величины Х1, X2, …, Xn называется независимыми, если закон распределения каждой из этих величин не зависит от того, какие значения приняли остальные величины.
Свойство 4.Если Х и Y независимые величины, то мат. ожидание их произведения равно произведению их мат. ожиданий: M(XY) = M(X)M(Y).
Свойство 5.Для случайных величин Х и Y верно равенство M(X+Y)=M(X)+M(Y).
Свойства 4,5 несложно распространить на любое число сомножителей и слагаемых. Биномиальную величину Х можно представить в виде суммы n независимых величин Xi, принимающих значение 1 с вероятностью p и 0 с вероятностью q, (Xi – число появлений событий в одном i-ом испытании). Поскольку M(Xi)=p, то верно следующее утверждение.
Следствие. Математические ожидание биномиальной величины Х с параметрами n и p равно M(X)=np.
5.3. Дисперсия и ее свойства
Дисперсия характеризует средневзвешенные отклонения в квадрате значений случайной величины относительно ее математического ожидания.
Определение. Дисперсией случайной величины Х называется математическое ожидание квадрата отклонения этой величины относительно ее математического ожидания.
Обозначение: D(X)=M((X-M(X))2).
Теорема.Дисперсия случайной величины Х равна D(X)=M(X2)–M(X)2.
Заметим, что по сравнению с исходной величиной 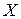 , дисперсия измеряется в квадратных единицах, поэтому наряду с ней рассматривается также среднее квадратичное отклонение (СКО) случайной величины, которые определяется как квадратный корень из ее дисперсии:
, дисперсия измеряется в квадратных единицах, поэтому наряду с ней рассматривается также среднее квадратичное отклонение (СКО) случайной величины, которые определяется как квадратный корень из ее дисперсии: 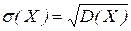 .
.
СКО измеряется в тех же единицах, что и исходная величина и характеризует средневзвешенное отклонение величины относительно ее математического ожидания. Перечислим основные свойства дисперсии и СКО.
Свойство 1.Дисперсия и СКО случайной величины Х неотрицательны:
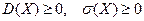
Свойство 2.Дисперсия (и СКО) ДСB Х равны нулю только в том случае, когда Х–постоянная.
Свойство 3.Если X –ДCB, а С число, то
D(CX )= C2D(X), 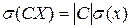
Свойство 4.Дисперсия суммы независимых величин равна сумме их дисперсий:
D(X+Y)=D(X)+D(Y), 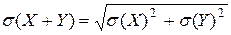
Свойство 5. Если Х–ДСВ а С– число, то D(C+X)=D(X)
Свойство 6. Для независимых величин X и Y: D(X–Y)=D(X)+D(Y).
Следствие 7. Дисперсия биномиальной случайной величины Х с параметрами n и p равна 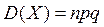 .
.
Выводы. По данной теме нами были рассмотренызакон распределения дискретной случайной величины, основные примеры, математическое ожидание ДСВ и его свойства, дисперсия ДСВ и ее свойства.
Дата добавления: 2015-10-21; просмотров: 3623;
