А) Построение третьего вида по двум заданным.

Содержание задания.

Построить третий вид детали по двум данным, проставить размеры, выполнить наглядное изображение детали в аксонометрической проекции. Задание взять из таблицы 6. Образец выполнения задания (рис. 5.19).

Графическую работу выполнить на листе чертежной бумаги формата А3.

Методические указания.

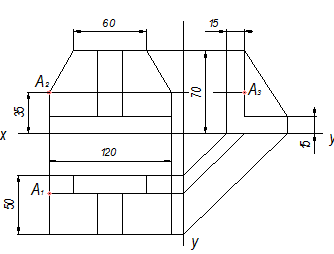
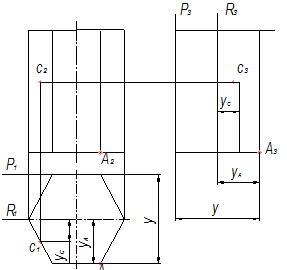
1. Выполнение чертежа начинают с построения осей симметрии видов. Расстояние между видами, а также расстояние между видами и рамкой чертежа принимают: 30-40 мм. Строят главный вид и вид сверху, Два построенных вида используют для вычерчивания третьего вида – вида слева. Этот вид чертится по правилам построения третьих проекций точек, для которых две другие проекции заданы (см. рис. 5.4 точка А). При проецировании детали сложной формы приходится одновременно вести построение всех трех изображений. При построении третьего вида в данном задании, как и в последующих, можно не наносить оси проекций, а воспользоваться «безосной» системой проецирования. За координатную плоскость можно принять одну из граней (рис. 5.5, плоскость Р), от которой отсчитываются координаты. Например, измерив отрезок на горизонтальной проекции для точки А, выражающий координату Y , переносим его на профильную проекцию, получаем профильную проекцию А₃. В качестве координатной плоскости можно взять также плоскость R симметрии, следы которой совпадают с осевой линией горизонтальной и профильной проекции, и от нее вести отсчет координат Y_С , Y_А , как показано на рис. 5.5, для точек А и С.

Рис. 5.4 Рис. 5.5

2. Каждую деталь, как бы сложна она ни была, всегда можно разбить на ряд геометрических тел: призму, пирамиду, цилиндр, конус, сферу и т.д. Проецирование детали сводится к проецированию этих геометрических тел.

3. Размеры предметов нужно наносить только после построения вида слева, так как во многих случаях именно на этом виде бывает целесообразно нанести часть размеров.

4. Для наглядного изображения изделий или их составных частей в технике применяют аксонометрические проекции. Рекомендуется предварительно изучить в курсе начертательной геометрии главу «Аксонометрические проекции».

Для прямоугольной аксонометрической проекции сумма квадратов коэффициентов (показателей) искажения равна 2, т.е.

k² + m² + n² =2,

где k, m, n –коэффициенты (показатели) искажения по осям. В изометрической

проекции все три коэффициента искажений равны между собой, т.е.

k = m = n = 0,82

Практически для простоты построений изометрической проекции коэффициент (показатель) искажения, равный 0,82, заменяют приведенным коэффициентом искажения, равным 1, т.е. строят изображение предмета, увеличенное в 1/ 0,82 = 1.22 раза. Оси X, Y, Z в изометрической проекции составляют между собой углы 120°, при этом ось Z направляют перпендикулярно к горизонтальной линии (Рис. 5.6).

В диметрической проекции два коэффициента искажения равны между собой, а третий в частном случае принимается равным 1/2 из них, т.е.,

k = n = 0,94; а m =1/2 k = 0,47

Практически для простоты построений диметрической проекции коэффициенты (показатели) искажения, равные 0,94 и 0,47, заменяют приведенными коэффициентом искажения, равным 1 и 0,5, т.е. строят изображение предмета, увеличенное в 1/ 0,94 = 1.06 раза. Ось Z в прямоугольной диметрии направлена перпендикулярно к горизонтальной линии, ось Х – под углом 7°10', ось Y – под углом 41°25'. Так как tg 7°10' ≈ 1/8, а tg 41°25' ≈ 7/8, то строить эти углы можно без транспортира, как показано на Рис. 5.7. В прямоугольной диметрии по осям Х и Z откладывают натуральные размеры, а по оси Y с коэффициентом сокращения 0,5.

Аксонометрическая проекция окружности в общем случае есть эллипс. Если окружность лежит в плоскости, параллельной одной из плоскостей проекций, то малая ось эллипса всегда параллельна аксонометрической прямоугольной проекции той оси, которая перпендикулярна к плоскости изображаемой окружности, большая же ось эллипса всегда перпендикулярна малой.

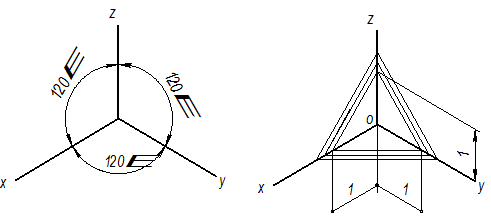
Рис. 5.6

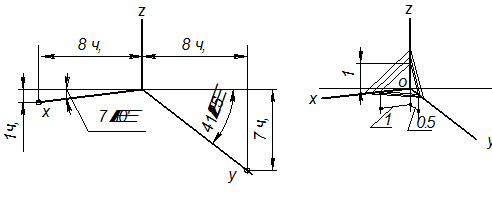
Рис. 5.7

В данном задании наглядное изображение детали рекомендуется выполнить в изометрической проекции.