Аксиоматика теории вероятностей

Предложенное выше классическое определение вероятности наряду с очевидными достоинствами, прежде всего простотой и интуитивной наглядностью, имеет и ряд существенных недостатков: предусматривает только конечное или счетное множество элементарных событий и обязательно знание их вероятностей. Всё это далеко не всегда имеет место, и поэтому введенное определение не является достаточно общим. В настоящее время стало общепринятым аксиоматическое построение теории вероятностей.

В математике аксиомами называются предложения, которые принимаются за истинные и в пределах данной теории не доказываются. Все остальные положения этой теории должны выводится чисто логическим путем из принятых аксиом. Формулировка аксиом представляет собой не начальную стадию развития математической науки, а является результатом длительного накопления фактов и логического анализа полученных результатов с целью выявления действительно основных первичных фактов. Именно так складывались аксиомы геометрии. Подобный же путь прошла и теория вероятностей, в которой аксиоматическое построение ее основ явилось делом сравнительно недавнего прошлого. Впервые задача аксиоматического построения теории вероятностей была решена в 1917 году советским математиком С.Н. Бернштейном.

В настоящее время общепринята аксиоматика академика А.Н. Колмогорова (1933 г.), которая связывает теорию вероятностей с теорией множеств и метрической теорией функций.

В аксиоматике А.Н. Колмогорова первичным является пространство (множество) элементарных исходов Ω. Что представляют собой элементы этого множества для логического развития теории вероятностей – безразлично. Далее рассматривается некоторая система F подмножеств множества Ω; элементы системы F называются случайными событиями. Относительно структуры системы F предполагаются выполненными три следующих требования:

1. Подмножество F в качестве элемента содержит достоверное событие Ω.

2. Если А и В – два события, определенные на Ω, входят в подмножество F в качестве элементов, то в качестве элементов подмножество F также содержит А+В, А∙В,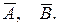

3. Если события А₁, А₂, …, определенные на Ω, являются элементами подмножества F, то их сумма 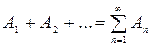и произведение 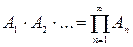также являются элементами подмножества F.

Множество F, образованное описанным выше способом называют «σ-ал-геброй событий».

Теперь перейдем к формулировке аксиом, определяющих вероятность.

Аксиома 1. (аксиома существования вероятности). Каждому случайному событию А из σ-алгебры событий F поставлено в соответствие неотрицательное число р(А), называемое его вероятностью.

Аксиома 2. (вероятность достоверного события). Вероятность достоверного события равна 1: Р(Ω)=1. (1.15)

Аксиома 3. (аксиома сложения). Если события А и В несовместны, то

Р(А+В) = P(А)+Р(В). (1.16)

Аксиома 4. (расширенная аксиома сложения). Если событие А равносильно наступлению хотя бы одного из попарно несовместных событий А₁, А₂, …, то есть, 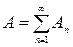, то вероятность события А равна

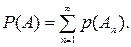(1.17)

Вероятность события Р(А) – численная мера степени объективной возможности этого события, удовлетворяющая вышеуказанным аксиомам.

Первые три аксиомы определяют вероятность.

Необходимость расширенной аксиомы сложения (аксиомы 4) связана с тем, что в теории вероятностей постоянно приходится рассматривать события, подразделяющиеся на бесконечное число частных случаев. Выведем из них несколько следствий, которые в некоторых учебниках представляются теоремами.