Противоположные события. Теорема. Доказательство. Примеры
Противоположными называют два единственно возможных события, образующих полную группу. Если одно событие обозначено А (или В), то противоположное ему событие принято обозначать 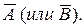
Пример 1.41. Попадание и промах при выстреле по цели – противоположные события. Если А – попадание, то 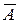 - промах.
- промах.
Пример 1.42. Из ящика наугад взята деталь. События {появилась стандартная деталь} и {появилась нестандартная деталь}- противоположные.
Рассмотрим некоторое случайное событие А, и пусть его вероятность известна.
Теорема. Если вероятность некоторого случайного события А известна и равна Р(А), то вероятность противоположного события 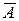 определяется по формуле
определяется по формуле  (1.18)
(1.18)
Доказательство. Согласно аксиоме 3 (формула 1.16) для несовместных событий Р(А+В) = Р(А) + Р(В).
В силу несовместности событий А и 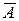 , и так как они образуют полную группу, согласно (1.15), (1.16) можем записать
, и так как они образуют полную группу, согласно (1.15), (1.16) можем записать
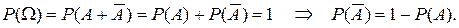
Следствие. 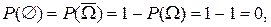 то есть вероятность невозможного события равна нулю.
то есть вероятность невозможного события равна нулю.
Примечание 1.Если вероятность одного из двух противоположных событий обозначена через р, то вероятность другого события обозначают через q. Согласно предыдущей теореме можем записать q = 1- p. (1.18-а)
Отсюда следует запись p + q = 1, то есть сумма вероятностей противоположных событий равна единице.
С помощью формулы (1.18-а) определяется, например, вероятность промаха, если известна вероятность попадания (или, наоборот, вероятность попадания, если известна вероятность промаха): например, если вероятность попадания для орудия 0,9, вероятность промаха для него 1- 0,9 = 0,1.
Пример 1.43. Завод производит 85% продукции первого сорта и 10% - второго. Остальные изделия считаются браком. Какова вероятность того, что взяв наугад изделие, мы получим брак?
Решение. Обозначим А – событие, заключающееся в том, что взятое изделие бракованное Задачу удобно решать, используя вышеизложенную теорему, то есть, через вероятность противоположного события 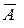 , заключающееся в том, что взятое изделие не бракованное, а первого или второго сорта. Вероятность этого события
, заключающееся в том, что взятое изделие не бракованное, а первого или второго сорта. Вероятность этого события 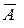 равно q=0,85+0,10=0,95. Тогда искомая вероятность равна р = 1 – q = 1– 0,95 = 0,05.
равно q=0,85+0,10=0,95. Тогда искомая вероятность равна р = 1 – q = 1– 0,95 = 0,05.
Пример 1.44.В ящике имеется п деталей, из которых m стандартных. Найти вероятность того, что среди k наугад извлеченных деталей естьхотя бы одна стандартная.
Решение. События «среди извлеченных деталей есть хотя бы одна стандартная» и «среди извлеченных деталей нет ни одной стандартной»— противоположные. Обозначим первое событие через А, а второе— через  .
.
Очевидно, Р(А)=1 - Р(  ). Найдем Р(
). Найдем Р(  ). Общее число способов, которыми можно извлечь k деталей из n деталей, равно
). Общее число способов, которыми можно извлечь k деталей из n деталей, равно 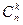 . Число нестандартных деталей равно n-т; из этого числа деталей можно
. Число нестандартных деталей равно n-т; из этого числа деталей можно 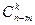 способами извлечь k нестандартных деталей. Поэтому вероятность того, что среди извлеченных k деталей нет ни одной стандартной, равна Р(
способами извлечь k нестандартных деталей. Поэтому вероятность того, что среди извлеченных k деталей нет ни одной стандартной, равна Р(  ) =
) = 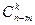 /
/ 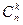 .Отсюда
.Отсюда 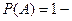
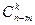 /
/ 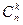 .
.
Дата добавления: 2015-10-30; просмотров: 2569;
