Вероятность произведения событий

Теорема. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого события, вычисленную при предположении, что первое событие уже наступило:

P(АВ)=Р(А)∙Р(В|А) (1.23)

Доказательство. По определению условной вероятности (формула (1.22)) имеем P(B|A) = P(AB)/P(A). Отсюда, предполагая, что р(А)≠0, р(В|А)≠0, можно получить P(АВ)=Р(А)∙Р(В|А), отсюда следует справедливость формулы (1.23) или рассматриваемой теоремы.

Примечание. Применив формулу (1.23) к событию ВА, получим P(BА)= P(В)∙Р(А|В). Поскольку событие ВА не отличается от события АВ, можем записать P(АВ)=P(В)∙Р(А|В), то есть,

Р(А)∙Р(В|А) = Р(B)∙Р(A|B) (1.24)

Формула (1.23) может быть обобщена на любое число событий

Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальныхсобытий, причем вероятность каждого последующего события вычисляется при предположении, что все предыдущие события уже появились: P(A₁А₂А₃…А_n)= Р(А₁)∙Р(A₂|А₁)∙Р(A₃|А₁A₂)∙Р(A₄|А₁А₂A₃) …

…∙Р(A_n| А₁ А₂ A₃ … А_n-1) (1.25)

где Р(A_n| А₁А₂A₃…А_n-1) – вероятность события A_n, вычисленная при предположении, что события А₁, А₂, A₃, …А_n-1 наступили. В частности, для трех событий формула (1.25) имеет вид

Р(АВС)=р(А)∙р(В|А)∙р(С|АВ) (1.25-а)

Пример 1.51. По условиям предыдущего примера 1.50 найти вероятность успешной сдачи экзамена, если для этого студент должен ответить на первый билет, или, не ответив на первый, обязательно ответит на второй.

Решение. Пусть события А = {первый билет «хороший»}, B= { второй билет «хороший» }. Тогда 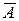={ первый билет «плохой»}. Экзамен будет сдан, если произойдет событие А, или одновременно 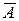и В. То есть искомое событие С={успешная сдача экзамена} выражается следующим образом: С = А + 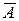В. Отсюда

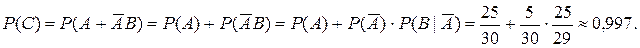
Здесь мы воспользовались несовместимостью А и 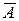, а следовательно, несовместимостью А и 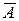В, теоремами о вероятности суммы и произведения и классическим определением вероятности при подсчете р(А) и р( ).

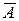Эту задачу можно решить и проще, если воспользоваться теоремой о вероятности противоположного события:

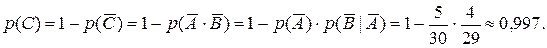
Пример 1.52. У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял наугад один валик, затем – другой. Найти вероятность того, что первый из взятых валиков конусный, а второй – эллиптический.

Решение. Пусть событие А = {первый валик конусный}, событие В = {второй валик эллиптический}.

Вероятность события А (первый валик - конусный ) равна Р(А) = 3/10.

Условная вероятность события В (второй валик эллиптический при предположении, что первый конусный) равна Р(В|А) = 7/9.

По теореме произведения (формула 1.23) искомая вероятность

Р(АВ) = Р(А)∙Р(В|А) = (3/10)∙(7/9) = 7/30.

Заметим, что, сохранив обозначения, легко найдем: Р(В) = 7/10, Р(А|В)=3/9, отсюда Р(В) Р(А|В) = 7/30, что наглядно иллюстрирует справедливость формулы (1.24).

Домашнее задание: ДР-6 ( №1.26,Письменный, стр. 39)

ДР-7 ( №3.18,Зарубин, стр. 110)