Которую называют формулой полной вероятности
Доказательство. Воспользуемся тем, что Hi (гипотезы) попарно несовместны (следовательно, несовместны и Hi∙А), и что их сумма есть достоверное событие
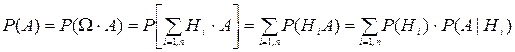(1.35)
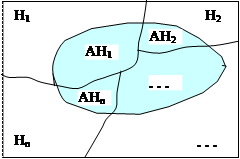
Эта схема имеет место всегда, когда можно говорить о разбиении всего пространства событий на несколько, вообще говоря, разнородных областей, в каждой из которых имеется некоторая совокупность элементарных событий АНi, благоприятствующих появлению события А (рис. 1.11.2, где область, соответствующая событию А, заштрихована).
|
Математическая модель может быть, например, такой: имеется несколько урн разного состава; в первой урне n1 шаров, из них m1 белых и т.д. По формуле полной вероятности находится вероятность того, что, выбрав урну наугад, достанем из нее белый шар.
В экономике это, например, разбиение страны или района на регионы разного размера и разных условий, когда известна доля каждого района р(Hi) и вероятность (доля) какого-то параметра в каждом регионе (например, процент безработных –в каждом регионе он свой) – р(А|Hi).
На складе может лежать продукция с трех разных заводов, поставляющих разное количество продукции с разной долей брака и т.д.
Пример 1.61. Литье в болванках поступает из 2-х цехов: 70% из первого и 30% из второго. При этом продукция первого цеха имеет 10% брака, а второго – 20%. Найти вероятность того, что одна, взятая наугад, болванка имеет дефект.
Решение. Вероятность того, что взятая болванка поступила из 1-го цеха, равна Р(Н1) = 0,7; вероятность того, что взятая болванка поступила из 2-го цеха, равна р(Н2) = 0,3. Вероятность того, что болванка из 1-го цеха бракованная, равна р(А|Н1) = 0,1; вероятность того, что болванка из 2-го цеха бракованная, равна р(А|Н2) = 0,2.
Тогда искомая вероятность того, что взятая наугад деталь бракованная, равна
Р(А) = 0,7∙0,1 + 0,3∙0,2 = 0,13 (в среднем 13% болванок с цехе дефектны).
По этой же схеме решаются задачи и в общем случае.
Пример 1.62. Вернемся к примеру 1.49 (раздел 1.10.4) с урной, в которой лежит N шаров, из которых n белых. Достаем из нее (без возвращения) два шара. Какова вероятность того, что второй шар белый?
Решение. Обозначим событие Н1 = {первый шар белый}; вероятность этого события Р(Н1) = n/N. Событие Н2 = {первый шар черный}; вероятность события Р(Н2) = (N-n)/N; событие A = {второй шар белый}.
Условные вероятности события А равны Р(А|Н1) = (n-1)/(N-1); Р(А|Н2) = n/(N-1).
Искомая вероятность
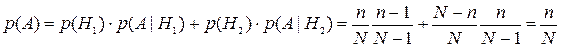
Эта модель может быть применена при решении такой задачи: из N билетов студент выучил только n. Что ему выгоднее – тянуть билет самым первым или вторым? Оказывается, в любом случае он с вероятностью n/N вытянет хороший билет и с вероятностью (N-n)/N плохой.
Домашнее задание: ДР-10 (Письменный, №1.29, , стр. 45)
Формула Байеса
Предположим, что событие А может произойти при условии появления одного из несовместных событий (гипотез) Hi , известны вероятности этих гипотез р(Hi) и условные вероятностир(А|Hi). Дополнительно известно, что событие А произошло. Найдем вероятность того, что при этом была реализована гипотеза Hk. По определению условной вероятности
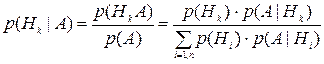(1.36)
Полученное соотношение называют формулой Байеса. Она позволяет по известным (до проведения опыта) априорным вероятностям гипотез р(Нi) и условным вероятностям р(А|Hi) определить условную вероятность р(Hi | А), которую называют апостериорной (то есть полученной при условии, что в результате опыта событие А уже произошло).
Пример 1.63. 30% пациентов, поступающих в больницу, принадлежат первой социальной группе, 20% – второй и 50% - третьей. Вероятность заболевания туберкулезом для представителя каждой социальной группы, соответственно, равна 0,02, 0,03 и 0,01. Проведенные анализы для случайно выбранного пациента показали наличие туберкулеза. Найти вероятность того, что это представитель третьей группы.
Решение. Пусть Н1, Н2, Н3 – гипотезы, заключающиеся в том, что пациент принадлежит соответственно первой, второй и третьей группам. Очевидно, что они образуют полную группу событий, причем р(Н1)=0,3, р(Н2)=0,2, р(Н3)=0,5. По условию событие А, обнаружение туберкулеза у больного, произошло, причем условные вероятности по данным условия равны Р(А|H1)=0,02, Р(А|H2)=0,03 и Р(А|H3)=0,01. Апостериорную вероятность Р(H3| А) вычислим по формуле Байеса:
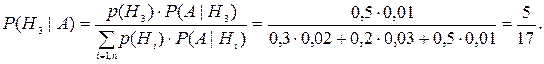
Домашнее задание: ДР-10 ( №1.29, Письменный, стр. 45)
ДР-11,12 ( №1.30, Письменный, стр. 46, №2, стр. 46,256)
Дата добавления: 2015-10-30; просмотров: 986;