Распределение Пуассона

Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А равна р. Для определения вероятности k появлений события А в этих испытаниях используется формула Бернулли. Если же n велико, то пользуются асимптотической формулой Муавра-Лапласа. Однако, эта формула непригодна, если вероятность события мала (р≤0,1). В этих случаях (n велико, р мало, а их произведение np<10) прибегают к асимптотической формуле Пуассона.

Сделаем допущение: произведение np сохраняет постоянное значение, то есть np=λ=сonst. Это означает, среднее число появлений события А в различных сериях испытаний, т.е. при различных значениях n, остается неизменным.

По формуле Бернулли интересующая нас вероятность равна

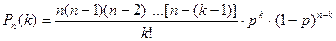
Так как np=λ, то p= λ/n. Следовательно,

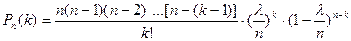
Так как n имеет очень большое значение, вместо Р_n(k) найдем 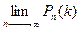. При этом будет найдено лишь приближенное значение отыскиваемой вероятности: хотя n и велико, но конечно при отыскании предела мы устремим n к бесконечности. Поскольку произведение np сохраняет свое постоянное значение, то при n→ ∞ вероятность р→0.

Итак,

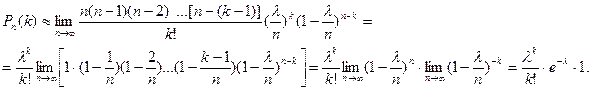
Таким образом, 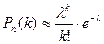(1.41)

Эта формула выражает закон распределения Пуассона вероятностей массовых (n велико) и редких (p мало) событий. Имеются специальные таблицы, пользуясь которыми можно найти P_n(k), зная k и λ.

Пример 1.69. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равно 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия.

Решение. По условию, n=5000, p=0,0002, k=3.

Найдем λ = np=5000·0,0002 = 1.

По формуле Пуассона искомая вероятность приближенно равна

Р₅₀₀₀(3)=λ^ke^-λ/k! = e^-1/3! = 1/(6·e) ≈ 0,06.

Домашнее задание: ДР-1.16( №1.32,Письменный, стр. 53)