Биномиальное распределение. Говорят, что случайная величина имеет биномиальное распределение с параметрами и , где , если принимает значения с вероятностями

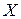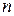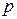Говорят, что случайная величина имеет биномиальное распределение с параметрами и , где 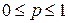, если 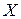принимает значения 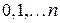с вероятностями 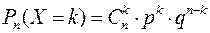. Случайная величина 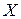с таким распределением имеет смысл числа успехов в 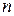испытаниях схемы Бернулли с вероятностью успеха .

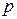Таблица распределения 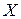имеет вид

			…	k	…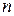
			…		…

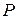
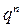
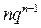
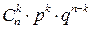
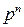
Пример.По мишени производится три выстрела, причём вероятность попадания при каждом выстреле равна 0,8. Рассматривается случайная величина 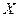– число попаданий в мишень. Найти закон её распределения.

Решение. По условию задачи случайная величина 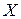может принимать только целые значения от 0 до 3, .

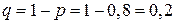Тогда:
,
,
,
.

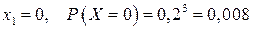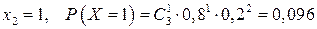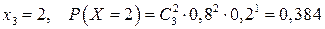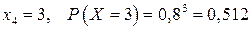Закон распределения (биномиальное распределение) примет вид:

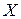
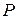
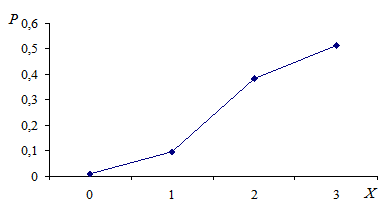
	0,008	0,096	0,384	0,512

Для проверки: 0,008+0,096+0,384+0,512=1.

График, соединяющий точки с координатами 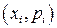называется многоугольником распределения (рис.1.).

Рис.1. Многоугольник распределения