Функция распределения СВ

Функцией распределения вероятностей случайной величины 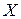называется функция некоторого аргумента 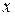, численное значение которой равно вероятности того, что случайная величина 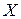примет значение, меньшее :

.

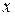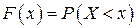Это определение справедливо как для дискретной, так и для непрерывной случайной величины.

Свойства функции распределения.

1. 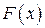есть неубывающая функция своего аргумента 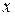, то есть если 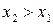, то .

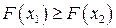2. , .

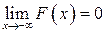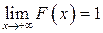3. 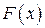принимает значения от 0 до 1: .

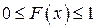4. Вероятность попадания случайной величины на заданный интервал 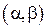равна разности значений функции:

.

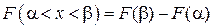Пример. Возьмем ряд распределения дискретной случайной величины Х из рассмотренного выше примера про попадания в мишень:

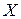
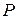
	0,008	0,096	0,384	0,512

Найти функцию распределения 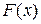, построить ее график.

Решение.

1) Если 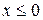, то 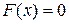. Действительно, значений, меньших, чем 0, случайная величина Х не принимает. Следовательно, при 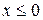функция распределения ;

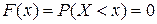2) Если 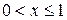, то ;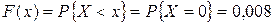

3) Если 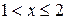, то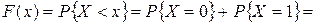

;

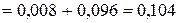4) Если 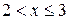, то ;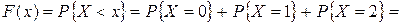

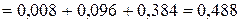5) Если 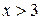, то ;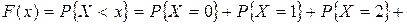

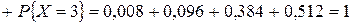Функция распределения ДСВ примет вид:

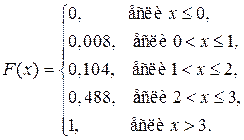
График функции распределения имеет вид (рис.2):

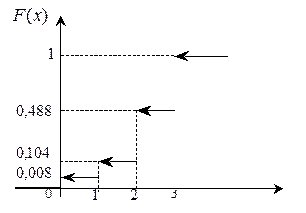
Рис.2. График функции распределения ДСВ

Замечание 1. Когда текущая переменная 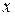проходит через какое-то из своих возможных значений, функция распределения меняется скачкообразно, причем величина скачка равна вероятности этого значения.

Замечание2. Функция распределения дискретной случайной величины имеет вид:

.

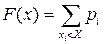Здесь суммирование ведется по всем 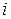, для которых .

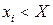В рассмотренном примере функцию распределения можно было бы записать следующим образом:

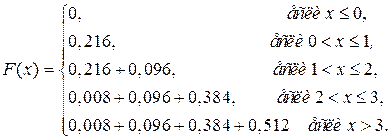
Функция распределения полностью характеризует случайную величину как дискретную, так и непрерывную. Функцию распределения еще называют интегральным законом распределения.