Математическое ожидание. «Случайных величин без мат
«Случайных величин без мат. ожидания не бывает, так как, если у нас есть случайная величина, мы всегда в праве от нее что-нибудь ожидать».
Из студенческой контрольной работы.
Математическим ожиданием дискретной случайной величины 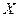 называется сумма произведений всех возможных значений случайной величины на вероятности этих значений:
называется сумма произведений всех возможных значений случайной величины на вероятности этих значений:
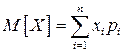 .
.
Замечание. Если число возможных значений СВ бесконечно, то математическое ожидание равно сумме ряда, если этот ряд сходится абсолютно:
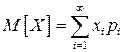 .
.
Пример.Распределение ДСВ задано рядом распределения
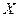
| |||
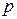
| 0,3 | 0,5 | 0,2 |
Математическое ожидание 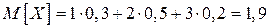 .
.
Математическое ожидание случайной величины есть ЧИСЛО!
Математическое ожидание приближенно равно среднему значению СВ, с тем большей точностью, чем больше число измерений. Поэтому математическое ожидание называют часто просто средним значением случайной величины.
Отметим, что математическое ожидание случайной величины всегда определяется однозначно и уже не является величиной случайной.
Математическим ожиданием 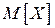 непрерывной случайной величины
непрерывной случайной величины 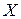 , распределенной на промежутке
, распределенной на промежутке 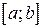 с плотностью распределения
с плотностью распределения 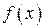 называется определенный интеграл от произведения плотности СВ на
называется определенный интеграл от произведения плотности СВ на 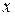 :
:
 .
.
Если же непрерывная случайная величина 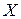 распределена на промежутке
распределена на промежутке  , то
, то 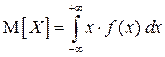 .
.
Если же 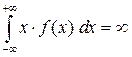 , то говорят, что математическое ожидание не существует.
, то говорят, что математическое ожидание не существует.
Свойства математического ожидания:
1. Математическое ожидание постоянной величины равно самой величине: 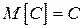 .
.
2. Постоянную 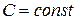 можно вынести за знак математического ожидания:
можно вынести за знак математического ожидания: 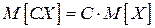 .
.
3. Математическое ожидание суммы двух СВ 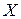 и
и  равно сумме математических ожиданий этих величин:
равно сумме математических ожиданий этих величин: 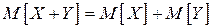 .
.
4. Математическое ожидание произведения двух независимых СВ равно произведению математических ожиданий этих величин: 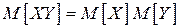 .
.
Пример.Найти математическое ожидание непрерывной случайной величины, если известна плотность распределения: 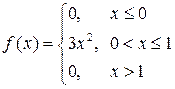 .
.
Решение. По определению получаем:
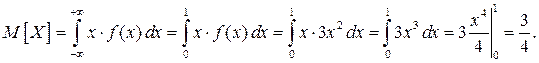
Пример. Найти математическое ожидание случайной величины 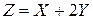 , если известны математические ожидания
, если известны математические ожидания 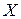 и
и 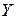 :
: 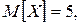
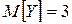 .
.
Решение. Используя свойства математического ожидания (математическое ожидание суммы равно сумме математических ожиданий слагаемых; постоянный множитель можно выносить за знак математического ожидания), получим:
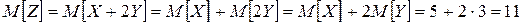 .
.
Дата добавления: 2015-10-19; просмотров: 2099;
