Задача синтеза (оптимизации) одноканальной замкнутой системы массового обслуживания с ожиданием.
Пусть исследуется одноканальная система массового обслуживания. для которой известные характеристики канала обслуживания и характеристики требований, которые поступают на обслуживание. необходимо определить оптимальную структуру системы, то есть оптимальное число требований 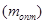 , необходимых для обслуживания канала, чтобы эффективность системы была максимальной. В качестве критерия оптимизации примем удельные приведенные затраты, которые характеризуют затраты всей системы на одно обслуживание. Аналитически выражение критерия оптимизации для определения оптимальной структуры одноканальной замкнутой системы массового обслуживания с ожиданием запишется следующим образом:
, необходимых для обслуживания канала, чтобы эффективность системы была максимальной. В качестве критерия оптимизации примем удельные приведенные затраты, которые характеризуют затраты всей системы на одно обслуживание. Аналитически выражение критерия оптимизации для определения оптимальной структуры одноканальной замкнутой системы массового обслуживания с ожиданием запишется следующим образом:
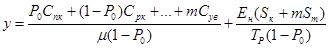
где 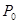 - вероятность простоя канала обслуживания
- вероятность простоя канала обслуживания
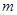 - число требований, которые требуют обслуживания
- число требований, которые требуют обслуживания
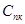 - средние затраты при простое канала обслуживания в продолжение часа из-за несвоевременного поступления требования на обслуживание
- средние затраты при простое канала обслуживания в продолжение часа из-за несвоевременного поступления требования на обслуживание
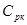 - средние затраты при работе канала обслуживания в продолжение часа
- средние затраты при работе канала обслуживания в продолжение часа
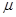 - интенсивность канала обслуживания
- интенсивность канала обслуживания
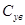 - средние затраты удержания требования в продолжение часа
- средние затраты удержания требования в продолжение часа
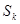 и
и 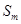 - капитальные вложения соответственно на канал обслуживания
- капитальные вложения соответственно на канал обслуживания
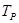 - годовой режим работы , то есть число часов работы в год
- годовой режим работы , то есть число часов работы в год
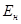 - нормативный коэффициент нормирования.
- нормативный коэффициент нормирования.
При определенные оптимальной структуры системы массового обслуживания, можно предположить:
Вероятность поступления определенного количества требований в систему зависит от длины периода поступления, а не от расположения этого периода, так как поток поступления требований на обслуживание - стационарный, а именно: число требований, которые поступили в систему в некоторый момент времени, не зависит от числа, которое поступило до того. Вероятность поступления двух или большее требований в один момент времени настолько маленькая, что ею можно пренебречь, а значит поток требований можно считать ординарным. Используя раньше полученные зависимости, получаем:
- вероятность того, что в системе на обслуживании находятся 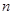 требований:
требований:
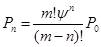 , где
, где 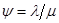
величина 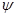 называется коэффициентом использования, где
называется коэффициентом использования, где 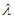 - интенсивность поступления,
- интенсивность поступления, 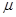 - интенсивность обслуживания
- интенсивность обслуживания
- вероятность простоя канала обслуживания:
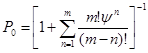
Дата добавления: 2015-11-01; просмотров: 1083;
