Исследование математической модели. Ограничимся исследованием режима работы, что установился замкнутой одноканальной системы
Ограничимся исследованием режима работы, что установился замкнутой одноканальной системы. Тогда:
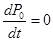 (n=0,1,...)
(n=0,1,...)
Действительно, вместо системы дифференционных уравнений получаем систему алгебраических уравнений:
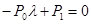
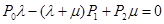
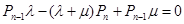
Используя полученную систему алгебраических уравнений легко выразить вероятности состояния системы в виде квадратной рекурентной формулы . Из первого уравнения определяется вероятность присутствия одного требования в системе.
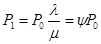
Из второго уравнения вероятность присутствия двух требований в системе:
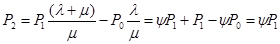
И в результате получаем:
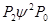
Аналогично проводится преобразование для 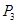
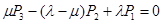
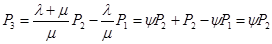
И наконец, суммируем полученные значения 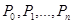 и находим суму:
и находим суму:
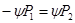
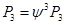
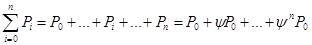
Используя формулу геометрической прогрессии, получаем:
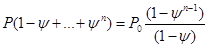
и при 
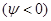 , сумма:
, сумма:
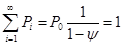
Откуда мы имеем:
1) вероятность простоя канала обслуживания:
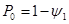
2) находим вероятность того, что в системе находится 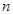 требований:
требований:
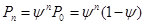
3) среднее число требований, которые находятся в системе:
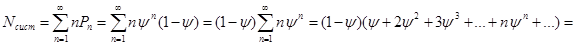
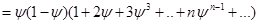
Последняя скобка есть производной от следующего выражения:
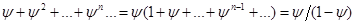
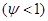 ,
,
то есть это выражение равняется:
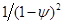
В результате получаем:
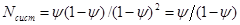
4) Дале находим среднее число требований, которые находятся в очереди:
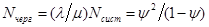
5) Находим среднее время ожидания требования в системе, который возможно определить, зная среднее число требований, которые находятся в системе:
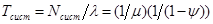
Задача анализу замкнутой системы с ожиданием (потоки требований Пуассоновские)
Постановка задачи:
Пусть исследуется некоторая система массового обслуживания с ограниченным количеством требований в системе, то есть требования, которые обслуживаются, снова возвращаются в систему обслуживания. Интенсивность поступления одного требования в систему известная и равняется  . Интенсивность обслуживания также известная и равняется
. Интенсивность обслуживания также известная и равняется 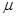 . Число требований, которые требуют обслуживания. равняется
. Число требований, которые требуют обслуживания. равняется 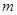 . Необходимо определить основные характеристики системы, а именно – вероятность того, что в системе есть
. Необходимо определить основные характеристики системы, а именно – вероятность того, что в системе есть 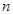 требований -
требований - 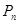 . Вероятность простоя канала обслуживания -
. Вероятность простоя канала обслуживания - 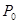 .Среднее число требований, которые находятся в очереди -
.Среднее число требований, которые находятся в очереди - 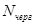 . Среднее число требований, которые находятся в системе -
. Среднее число требований, которые находятся в системе - 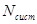 . Среднее время ожидания в очереди -
. Среднее время ожидания в очереди - 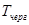 . Среднее время ожидания требования в системе -
. Среднее время ожидания требования в системе - 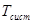 .
.
Состояние системы будем связывать с числом требований, которые находятся в системе. При этом возможные два состояния:
1) число требований, которые поступили в систему, равняется нулю 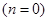 ,то есть каналы обслуживания простаивают.
,то есть каналы обслуживания простаивают.
2) число требований , которые поступили в систему 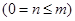 .
.
Зачеркнем размеченный граф состояний одноканальной замкнутой системы массового обслуживания с ожиданием:
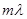
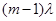
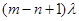
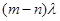

 |  |  |
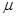
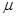
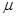
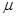
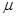
Дата добавления: 2015-11-01; просмотров: 614;
