Исследование математической модели
Для вычисления времени, через который очередь исчезнет, необходимо раскрыть математическую модель, а именно:
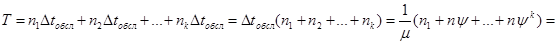
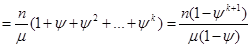
В модели использованная формула суммы геометрической прогрессии. Чем ближе интенсивность потока 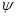 к интенсивности обслуживания
к интенсивности обслуживания 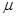 , тем через больший промежуток времени исчезнет очередь. Если величиной
, тем через больший промежуток времени исчезнет очередь. Если величиной 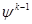 можно пренебречь для упрощения, тогда можем записать, что
можно пренебречь для упрощения, тогда можем записать, что
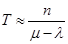
Задача анализу разомкнутой системы с ожиданием (потоки требований Пуассоновськие)
Постановка задачи:
Пусть данная некоторая система массового обслуживания, для которой справедливые следующие гипотезы:
1) вероятность поступления требований не зависит от принятого начала отсчета времени, а зависит только от времени периода наблюдение (поток стационарный)
2) не поступают в систему и не оставляют ее одновременно 2 или больше требований (поток стационарный)
3) поступление одной требования не зависит от поступления другой (отсутствие последействия). Известные также интенсивность  поступления потоков требований (среднее число обслуживание за единицу времени -
поступления потоков требований (среднее число обслуживание за единицу времени - 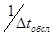 ). Нужно определить основные характеристики системы, а именно:
). Нужно определить основные характеристики системы, а именно:
- P – вероятность простоя канала обслуживания
- 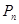 - вероятность того, что в системе находятся n-требований
- вероятность того, что в системе находятся n-требований
- 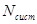 - среднее число требований, которые находятся в системе
- среднее число требований, которые находятся в системе
- 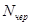 - среднее число требований, которые находятся в очереди
- среднее число требований, которые находятся в очереди
- 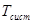 - среднее время ожидания требований в системе.
- среднее время ожидания требований в системе.
Поток требований, который владеет качествами стационарности, ординарности и отсутствием последействия, называют простым. В нашей задаче поток требований простой. Основным понятием при анализе процесса системы массового обслуживания есть состояние системы. Зная состояние системы, можно предусмотреть в вероятносном смысле ее поведение. Простой поток – это стационарный Пуассоновський поток. Если все потоки событий, которые переводят систему из одного состояния к другому являются Пуассоновськими, то для этих системы вероятность состояния описывается с помощью систем обычных дифференционных уравнений. В большинства задач не прикладного характера замена непуассоновського потока событий Пуассоновським с теми же интенсивностями приводит к получению решения, которое мало отличаются от истинного, а иногда и совсем не отличается. В качестве критерия отличия реального стационарного потока от Пуассоновського можно рассматривать близость математического ожидания числа дисперсий событий, которые поступают на определенном участке времени в реальном потоке.
Существует определенный математический прием, который значительно облегчает вывод дифференционного уравнения для вероятностного состояния. Сначала строится размеченный граф состояний с указанием возможных переходов. Это облегчает исследование и делает его более наглядным. Граф состояний, на котором проставленные не только стрелки переходов, но и интенсивность соответствующих потоков событий называют размеченным.
Зачертим размеченный граф состояний одноканальной разомкнутой системы массового обслуживания с ожиданием:

|
|
|
|
|










 ........
........





 .........
.........
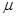
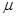
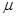
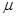
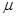
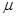
Если составленный размеченный граф состояний, то для построения математической модели, то есть для составления системы обычных дифференционных уравнений рекомендуется использовать следующие правила:
производная 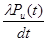 вероятности пребывания системе в состоянии n равняется алгебраической сумме следующих величин: число величин этой суммы равняется числу стрелок на графе состояний системы, которая соединяет состояние n с другими состояниями. Если стрелка направленная в состояние n, то соответствующая величина берется с знаком “+” . Если стрелка направленная из состояния n – то с знаком “-“. Каждая величина суммы равняется произведению вероятностей того состояния, из которого направленная стрелка на интенсивность потока событий, которые переводят систему по данной стрелке.
вероятности пребывания системе в состоянии n равняется алгебраической сумме следующих величин: число величин этой суммы равняется числу стрелок на графе состояний системы, которая соединяет состояние n с другими состояниями. Если стрелка направленная в состояние n, то соответствующая величина берется с знаком “+” . Если стрелка направленная из состояния n – то с знаком “-“. Каждая величина суммы равняется произведению вероятностей того состояния, из которого направленная стрелка на интенсивность потока событий, которые переводят систему по данной стрелке.
В соответствии с размеченным графом состояний, используя данное состояние, запишем систему обычных дифференционных уравнений вероятностей состояний таким образом:
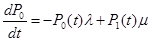 ;
;
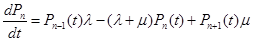
Дата добавления: 2015-11-01; просмотров: 655;
