Построение математической модели
В соответствии с размеченным графом состояния и правилом Колмагорова запишем систему обычных дифференционных уравнений для состояния системы.
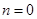
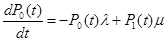
...................................................
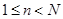
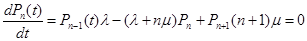
...................................................
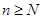
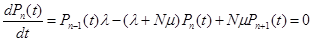
Ограничимся исследованием установившегося режима работы системы, если  - const,
- const, 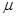 - const
- const
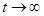 ,
, 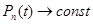
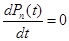
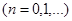
и тогда вместо системы обычных дифференциальных уравнений получаем систему алгебраических уравнений:
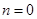
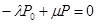
............................................
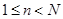
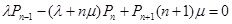
............................................
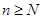
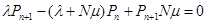
Используя полученные алгебраические уравнения, определим выражения для определения вероятности нахождение системы в состоянии 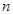 .
.
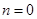
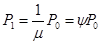
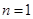
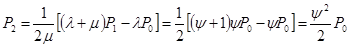
..............................................
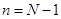
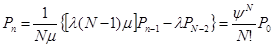
Из этих выражений видно, что при 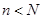 вероятность нахождения в системе
вероятность нахождения в системе 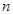 требований определяется по следующей формуле:
требований определяется по следующей формуле:
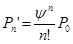
Для состояния 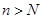 :
:
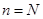
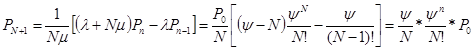 ;
;
...................................................
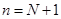
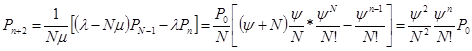
Из полученных выражений видно, что для составления системы, при 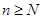 вероятность нахождения в системе
вероятность нахождения в системе 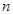 требований определяется по следующей формуле:
требований определяется по следующей формуле:
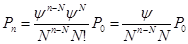
имея аналитическое выражение для всех состояний системы, а также используя очевидное равенство:
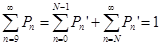
Определим вероятность простоя канала обслуживания:
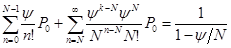
Вероятность простоя:
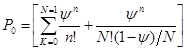
Среднее число требований, которые находятся в очереди, найдем по:
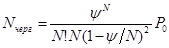
Среднее время ожидания заявок в очереди:
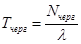
Среднее число занятых каналов :
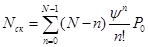
Задача анализу разомкнутой системы с отказом (потоки требований Пуассоновские)
Постановка задачи:
Пусть исследуется некоторая разомкнутая системы массового обслуживания, интенсивность поступления требований в систему известная и равняется  . Интенсивность обслуживания каждого канала известная и равняется
. Интенсивность обслуживания каждого канала известная и равняется 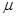 . Если требования застали все
. Если требования застали все 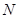 каналов занятыми, то они получают отказ и оставляют систему. Эта задача впервые рассматривалась Ерлангом. Необходимо определить
каналов занятыми, то они получают отказ и оставляют систему. Эта задача впервые рассматривалась Ерлангом. Необходимо определить
1) вероятность 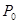 того, что все каналы обслуживания свободные;
того, что все каналы обслуживания свободные;
2) вероятность 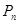 того, что занят равно
того, что занят равно 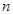 каналов обслуживания
каналов обслуживания
3) среднее число занятых каналов обслуживания
Зачеркнем разомкнутый граф состояний многоканальной разомкнутой системы массового обслуживания с отказом:












|
|
|
|
|





 ....... ........
....... ........
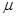
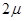
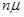
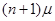
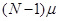
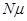
Состояние системы будем связывать с числом занятых каналов обслуживания. Пересчитаем основные возможности 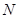 состояний системы:
состояний системы:
1) все каналы свободные. Ни одна требование не обслуживается
2) один канал занятый. Обслуживается одна заявка
...........................................................
n) 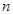 - каналов заняты. Обслуживается
- каналов заняты. Обслуживается 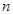 требований
требований
...........................................................
N) Все 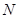 каналов заняты, обслуживается
каналов заняты, обслуживается 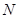 требований.
требований.
В соответствии с размеченным графом состояний, и используя правило Колмагорова, запишем систему обычных дифференционных уравнений для вероятности состояния системы:
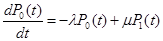
...................................................
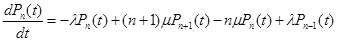
....................................................
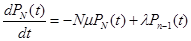
исследуя стационарный режим работы системы, при 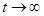 , система рекурентных алгебраических уравнений будет иметь вид:
, система рекурентных алгебраических уравнений будет иметь вид:
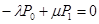
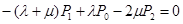
......................................................
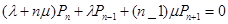
......................................................
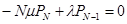
Из первого уравнения
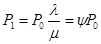
Аналогично, со второго:
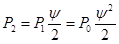
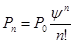
Используя полученные соотношения, возможно определить вероятность 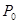 того, что все каналы обслуживания свободные.
того, что все каналы обслуживания свободные.
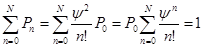
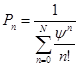
Вероятность того, что занято ровно 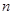 каналов обслуживания, будет равняться:
каналов обслуживания, будет равняться:
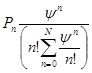
среднее число занятых каналов обслуживания:
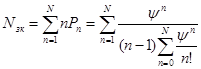
Задача анализу замкнутой системы с ожиданием (потоки требований Пуассоновские)
Постановка задачи:
Пусть исследуется некоторая система массового обслуживания, в которой требования, которые обслуживаются, снова возвращаются к системе обслуживания. Интенсивность одной требования - 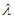 , интенсивность обслуживания каждого канала -
, интенсивность обслуживания каждого канала - 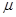 , число каналов обслуживания -
, число каналов обслуживания - 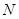 . Число требований, которые требуют обслуживания -
. Число требований, которые требуют обслуживания - 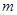 . Будем считать, что
. Будем считать, что 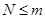 .
.
Необходимо определить:
1) вероятность того, что в системе находятся 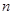 требований:
требований: 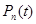
2) вероятность простоя каналов обслуживания 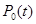
3) Среднее число требований, которые ожидают начала обслуживания, или длину очереди 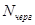
4) Среднее время ожидания требования в очереди 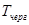
Состояние системы будем связывать с числом требований, которые находятся в системе. При этом возможные 2 случая:
1) Число требований 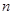 , которые поступили в систему, меньше числа каналов обслуживания, то есть
, которые поступили в систему, меньше числа каналов обслуживания, то есть 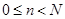
2) Число требований 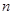 , которые поступили в систему, большее или равняется числу каналов обслуживания
, которые поступили в систему, большее или равняется числу каналов обслуживания 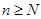
Из них 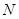 обслуживается, а
обслуживается, а 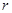 требований ожидают в очереди.
требований ожидают в очереди. 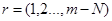
Зачертим граф состояний многоканальной замкнутой системы массового обслуживания с ожиданием
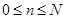 :
:
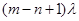
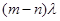
|
|
|
|
|
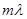
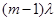










 ................
................
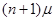
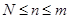
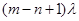
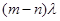
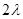
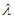
 | 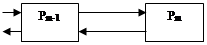 |
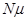
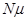
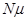
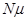
В соответствии с размеченным графом состояний системы, и используя правило Колмагорова, запишем дифференциальные уравнения для вероятности состояний системы:
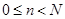
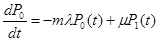
..................................................
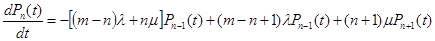
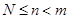
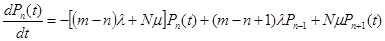
...................................................
Дата добавления: 2015-11-01; просмотров: 679;
