Математическое моделирование эмпирико-статистическим методом

Такое моделирование применяется в тех случаях, если априорной информации об объекте недостаточно. При построении математической модели на основе этого подхода различают активные и пассивные эксперименты. Пассивный эксперимент – это когда ставится большая серия опытов с поочередным колебанием каждой искомой переменной. Сюда же относят и сбор информации в режиме нормального функционирования. Обработка результатов проводится методами регрессионного и корреляционного анализа.

Активный эксперимент ведется по заранее составленному плану. Это разрешает существенно уменьшить количество опытов, и установить зависимости между переменными и условиями оптимума. Как в пассивном, так и в активном экспериментах математические модели описываются некоторыми функциями отклика:

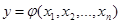
В данной записи 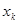будем называть факторами. Геометрически это некоторая поверхность отклика. При использовании статистических методов функцию отклика обычно отображают полиномиальным представлением (например, рядом Тейлора)

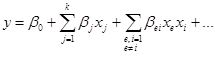
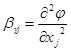
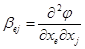
В реальном эксперименте рядом с управляемыми факторами 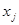всегда присутствуют неконтролируемые, отсюда функция отклика носит случайный характер. Поэтому при обработке экспериментальных данных вместо теоретических 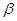коэффициентов получают их оценки, которые называются выборочными коэффициентами регрессии, а само уравнение - уравнением регрессии.

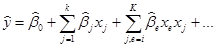
Коэффициенты регрессии обычно определяются на основе метода наименьших квадратов из условия минимума функционала:

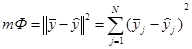
где 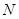- объем выборки из всего объема значений исследуемого параметра.

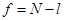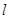Введем степень свободы , где - число связей, которые наложенные на выборку. Вид уравнения регрессии выбирается путем экспериментального подбора данных. Зачертим таблицу определения коэффициентов уравнения регрессии.

Метод наименьших квадратов предусматривает вычисление параметров для широкого круга функций, которые линейно зависят от этих параметров.

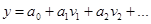
где 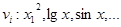- произвольная функция

Выборка в качестве оценок искомых параметров 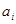предусматривает минимум следующего функционала:

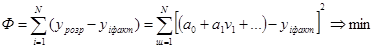
Здесь 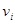и 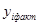- переменные, над которыми ведется наблюдение, 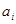- искомые неизвестные параметры функций.