Метод регрессионного анализа

Статистической называется зависимость, при которой изменение одной из величин приводит к изменению другой. Иногда такую зависимость называют корреляционной. Условным средним значением называют среднее арифметическое значение некоторой случайной величины 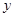, и соответствующее ей другое случайное значение 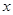. 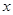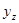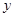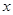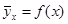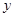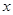Если каждому значению соответствует значение , то можно говорить, что случайная величина корреляционно зависит от величины и существует функциональная зависимость (1), то есть корреляционной зависимостью от называется функциональная зависимость (1).

Уравнение вида

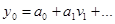
называется уравнением регрессии. Для проведения регрессионного анализа необходимое выполнение следующих условий:

1) Входной параметр 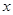вычисляется с довольно малой ошибкой. Ошибка функции отклика объясняется неучетом ряда переменных, которые не вошли в уравнения регрессии.

2) Результат наблюдения над входными величинами 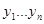являются независимыми нормальнораспределенными величинами.

3) При проведении опыта с объемом выборки 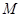, при условии, что каждый опыт проводится параллельно 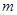раз, выборочные дисперсии 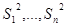должны быть однородными.

- Статистической называют гипотезу о виде неизвестного распределения, параметры известного распределения.

- Нулевой (основной) называют предположенную гипотезу и обозначают .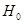

- Конкурирующей гипотезой 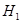называют гипотезу что противоречит гипотезе .

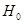- Так как выдвинутая гипотеза может быть верной или ошибочной, возникает необходимость ее проверки. При этом возникает ошибка 1-ого рода (если полностью отброшенная верная гипотеза)