Построение математической модели. В соответствии с размеченным графом состояний и используя правило Колмагорова, запишем систему дифференционных уравнений для вероятности состояния:
В соответствии с размеченным графом состояний и используя правило Колмагорова, запишем систему дифференционных уравнений для вероятности состояния:
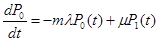 ;
;
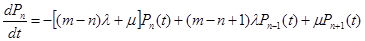
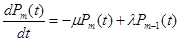
Ограничимся исследованием установившегося режима работы системы. Тогда:
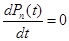 ,
, 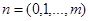
и вместо системы обычных дифференционных уравнений мы получаем систему алгебраических уравнений:
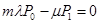
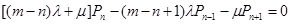
Для 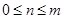 нетрудно получить рекурентную формулу:
нетрудно получить рекурентную формулу:
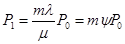 ; при
; при 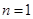
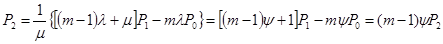 ; при
; при 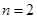
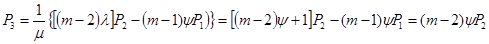
..........................................
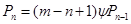 ;
;
Вероятность того, что в системе находится 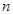 требований, будет равна:
требований, будет равна:
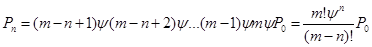
Используя равенство:
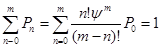
можно получить выражение для 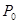 .
.
Вероятность простоя канала обслуживания 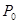 будет равняться:
будет равняться:
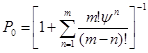
Среднее число требований, которые находятся в очереди, равняется:
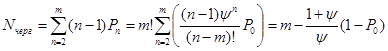
Среднее время ожидания требования в очереди:
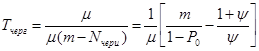
Среднее время ожидания требования в очереди:
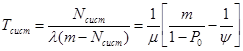 .
.
Как можно заметить, определение основных характеристик одноканальных систем массового обслуживания требует большой вычислительной работы, в связи с чем все расчеты делаются на компьютере.
Задача анализу многоканальной системы массового обслуживания .
Задача анализу разомкнутой системы с ожиданием ( потоки требований Пуассоновские)
Постановка задачи: пусть известные интенсивность  поступления потока требований в систему, и интенсивность
поступления потока требований в систему, и интенсивность 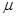 обслуживания этих требований. Число каналов обслуживания
обслуживания этих требований. Число каналов обслуживания 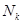 , и необходимо определить вероятность того, что в системе находятся
, и необходимо определить вероятность того, что в системе находятся 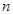 требований
требований 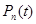 , вероятность простоя каналов обслуживания
, вероятность простоя каналов обслуживания 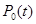 , среднее число требований, которые находятся в очереди. Среднее время ожидания
, среднее число требований, которые находятся в очереди. Среднее время ожидания 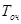 . Среднее число свободных каналов обслуживания.
. Среднее число свободных каналов обслуживания.
В этой задаче возможные два случая:
1) в системе 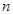 изменяется
изменяется 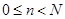
2) число требований 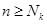 - числу каналов
- числу каналов
В первом случае все требования, которые находятся в системе, одновременно обслуживаются, и не все каналы занятые. Общая интенсивность обслуживания: 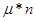
Зачеркнем размеченный граф состояний многоканальной разомкнутой системы массового обслуживания:









 |  |  |
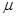
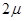
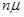
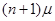
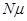
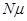
Дата добавления: 2015-11-01; просмотров: 682;
