VI. Элементы математической статистики
1. Характеристики распределения опытных данных
Задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов.
Вся подлежащая изучению совокупность объектов называется генеральной совокупностью.
Та часть объектов, которая попала на проверку, называется выборочнойсовокупностью или выборкой. Число элементов совокупности называется ее объемом. Наблюдаемые значения 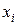 количественного признака
количественного признака 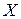 называются вариантами. Последовательность вариант, записанных в возрастающем порядке, называют вариационным рядом. Число
называются вариантами. Последовательность вариант, записанных в возрастающем порядке, называют вариационным рядом. Число 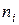 наблюдений значения
наблюдений значения 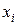 называется частотой варианты
называется частотой варианты 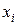 . Отношение частоты
. Отношение частоты 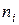 к объему выборки
к объему выборки 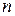 называется относительной частотой
называется относительной частотой 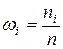 или частостью.
или частостью.
Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот.
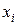
| 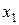
| 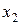
| … | 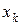
| 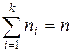
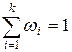
|
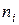
| 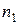
| 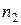
| … | 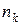
| |
| 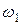
| 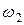
| … | 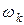
|
Эмпирической функцией распределения называют функцию 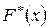 , определяющую для каждого значения
, определяющую для каждого значения 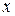 относительную частоту события
относительную частоту события 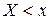
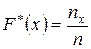 ,
,
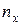 – число наблюдений, при которых наблюдалось значение признака
– число наблюдений, при которых наблюдалось значение признака 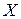 ,
,
меньшее 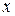 ,
,
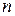 – общее число наблюдений (объем выборки).
– общее число наблюдений (объем выборки).
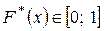 эмпирическая функция статистического распределения является аналогом интегральной функции случайной величины
эмпирическая функция статистического распределения является аналогом интегральной функции случайной величины 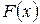 .
.
Полигоном частот называют ломаную, отрезки которой соединяют точки 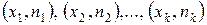 .
.
Полигоном относительных частот называют ломаную, отрезки которой соединяют точки 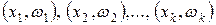 .
.
В случае непрерывного статистического распределения строят гистограмму. Гистограммой частот называют фигуру, являющуюся совокупностью прямоугольников, основания которых равны длинам интервалов 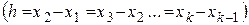 , а высоты равняются плотности частоты (т.е. отношению
, а высоты равняются плотности частоты (т.е. отношению 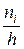 ). Гистограмма относительных частот строится в соответствии с плотностями относительных частот.
). Гистограмма относительных частот строится в соответствии с плотностями относительных частот.
Площадь гистограммы относительных частот равна единице. Это свойство идентично свойству вероятностей событий, образующих полную группу.
Накопленные частоты 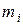 – это результаты последовательного суммирования частот всех вариант (или частот интервалов), включая частоту данного варианта (или интервала). Накопленные частоты показывают число членов совокупности, для которых признак не превышает данного значения.
– это результаты последовательного суммирования частот всех вариант (или частот интервалов), включая частоту данного варианта (или интервала). Накопленные частоты показывают число членов совокупности, для которых признак не превышает данного значения.
Кумулятивная кривая – это ломаная линия, отрезки которой соединяют точки 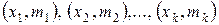 .
.
Средние величины рассматриваются в статистике как обобщающие показатели, в которых находят выражение действие общих для данного явления условий. Основной средней величиной является среднее арифметическое или выборочное среднее.
Выборочным средним 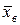 называют среднее арифметическое значение признака выборочной совокупности
называют среднее арифметическое значение признака выборочной совокупности
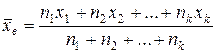 .
.
Свойства выборочного среднего:
1. 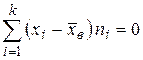 .
.
2. 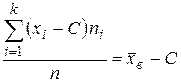 ,
,
или
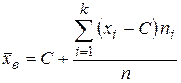 .
.
Медиана – это варианта, которая делит вариационный ряд на две части, равные по числу вариант.
Для дискретного вариационного ряда:
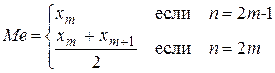
Для интервального вариационного ряда:
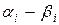
| 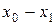
| 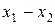
| … | 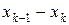
|
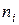
| 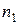
| 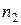
| … | 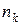
|
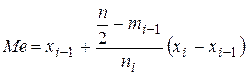 ,
,
где 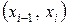 – медианный интервал, который выбирают по срединному значению,
– медианный интервал, который выбирают по срединному значению,
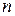 – объем выборки,
– объем выборки,
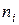 – частота медианного интервала,
– частота медианного интервала,
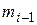 – сумма частот интервалов, предшествующих медианному.
– сумма частот интервалов, предшествующих медианному.
Модой называют значение варианты, имеющее наибольшую частоту.
Для дискретного вариационного ряда мода определяется непосредственно сравнением частот.
Для интервального вариационного ряда
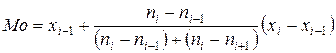 ,
,
где 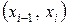 – модальный интервал с наибольшей частотой,
– модальный интервал с наибольшей частотой,
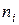 – частота модального интервала,
– частота модального интервала,
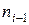 – частота интервала, предшествующего модальному,
– частота интервала, предшествующего модальному,
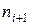 – частота интервала, следующего за модальным.
– частота интервала, следующего за модальным.
Показатели вариации
Вариация индивидуальных значений признака является атрибутивным свойством явления. В ней выражается то влияние множества случайностей, которое характерно для исследуемого явления. Показатели вариации вместе со средними величинами представляют тот фундамент, на который опирается математико-статистический анализ..
Размах вариации (или ее амплитуда) – это разность между наибольшим и наименьшим значениями признака
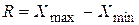 .
.
Среднее абсолютное или среднее линейное отклонение – это взвешенное частотами среднее из абсолютных отклонений вариант ряда от выборочного среднего
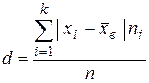 .
.
Выборочной дисперсией 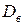 называют среднее арифметическое квадратов отклонений наблюдаемых значений признака от их среднего значения
называют среднее арифметическое квадратов отклонений наблюдаемых значений признака от их среднего значения 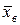
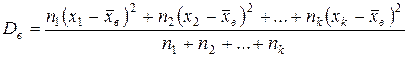
или
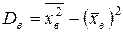 ,
,
где 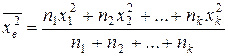 .
.
Средним квадратическим отклонением 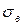 называют корень квадратный из дисперсии
называют корень квадратный из дисперсии 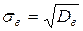 .
.
Линейный коэффициент вариации – это относительная характеристика степени колеблемости значений признака
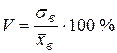 .
.
Коэффициент вариации служит для сравнения величин рассеяния двух вариационных рядов: тот из рядов имеет большее рассеяние, у которого коэффициент вариации больше.
| Пример 17. | Провести анализ статистического распределения выборки работников цеха по производительности труда (количество изготавливаемых за смену деталей) |
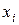
| ||||
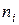
|
 |
Решение. Объем выборки
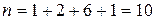 .
.
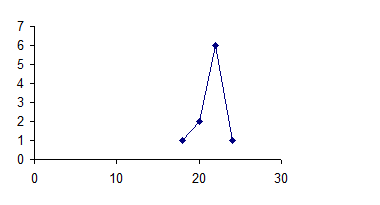
Полигон частот имеет вид:
Эмпирическая функция распределения
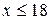
| 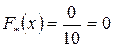
| 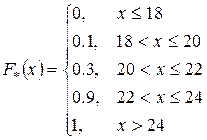
|
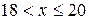
| 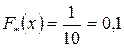
| |
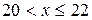
| 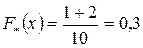
| |
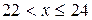
| 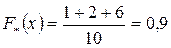
| |
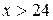
| 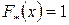
|
Выборочное среднее:
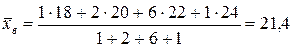 .
.
Медиана:
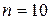 – четное число,
– четное число,
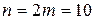 ,
, 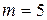 .
.
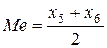 .
.
Найдем накопленные частоты
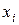
| ||||
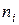
| ||||
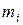
|
Начиная с четвертой по девятую, варианты имеют значение, равное 22. Следовательно, 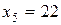 и
и 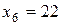 .
.
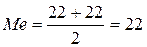 .
.
Мода:
наибольшая частота 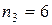 соответствует варианте 22.
соответствует варианте 22.
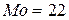 .
.
Размах вариации:
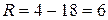 .
.
Среднее абсолютное отклонение:
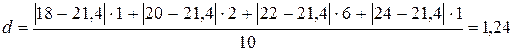 .
.
Выборочная дисперсия:
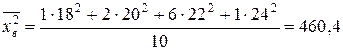 ,
,
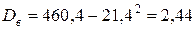 .
.
Среднее квадратическое отклонение:
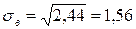 .
.
Коэффициент вариации:
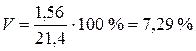 .
.
| Пример 18. | Построить полигон частот, определить моду и медиану интервального статистического распределения выборки колосьев пшеницы по их длине (мм). |
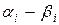
| 0 – 2 | 2 – 4 | 4 – 6 | 6 – 8 | 8 – 10 | 10 – 12 |
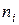
|
Решение.
Объем выборки:
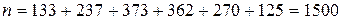 .
.
Полигон построим по серединам интервалов распределения:
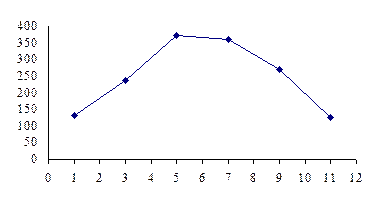 |
Найдем накопленные частоты:
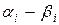
| 0 – 2 | 2 – 4 | 4 – 6 | 6 – 8 | 8 – 10 | 10 – 12 |
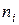
| ||||||
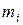
| ||||||
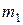
| 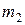
| 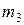
| 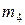
| 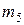
| 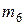
|
Медиана:
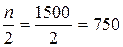
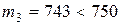 ,
, 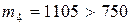 .
.
(6; 8) – медианный интервал.
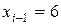 ,
, 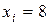 .
.
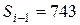 ,
, 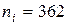 .
.
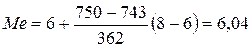 .
.
Мода:
наибольшая частота 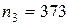 определяет модальный интервал (4;6).
определяет модальный интервал (4;6).
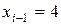 ,
, 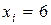 .
.
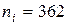 ,
, 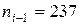 ,
, 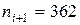 .
.
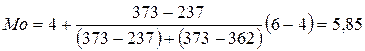 .
.
Дата добавления: 2015-10-13; просмотров: 5991;
