Пусть в результате испытания получен интервальный вариационный ряд признака
Значение показателя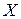 
| 
| 
| … | 
|
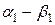
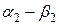
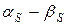
Частоты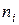 
| 
| 
| … | 
|
,
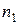
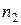
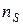
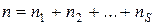который имеются основания считать распределенным по нормальному закону. Для построения нормального закона необходимо вычислить выборочную среднюю и дисперсию этого распределения. В соответствии с законом больших чисел выборочная средняя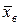 
является оценкой математического ожидания 
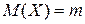, а дисперсия 
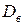– оценкой дисперсии 
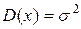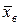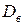искомого нормального закона. Нормальный закон с параметрами и будет теоретическим законом, который отображает распределение признака в генеральной совокупности.
| Пример. | Рост взрослых мужчин является случайной величиной, распределенной по нормальному закону. Найти общие выражения плотности вероятности и функции распределения за данными |
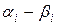
| 168-170 | 170-172 | 172-174 | 174-176 | 176-178 | 178-180 | 180-182 | 182-184 | 184-186 |
|
|
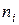
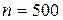. Заменим интервалы 
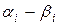на их середины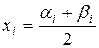 
| |||||||||
|
|
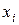
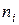
По формулам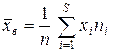 
и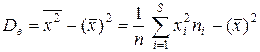 
вычисляем выборочную среднюю и дисперсию
.
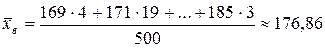
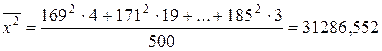
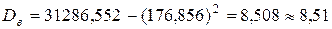Тогда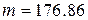 
, 
, 
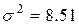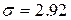. Плотность вероятности
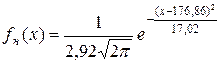
Функция распределения
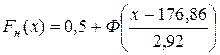
Дата добавления: 2015-10-13; просмотров: 1053;