Закон больших чисел. Принцип практической уверенности Если в определенных условиях вероятность события очень мала
| Принцип практической уверенности | Если в определенных условиях вероятность события очень мала, то при однократном их выполнении можно быть уверенным в том, что это событие не произойдет, и в практической деятельности поступать так, как будто оно является невозможным. Вероятность, которой решено |
пренебрегать в одном исследовании, называется уровнем значимости. В статистике обычно рекомендуется пользоваться уровнем значимости 0,05 при предварительных исследованиях и 0,01 при окончательных выводах.
Под законом больших чисел понимается совокупность положений, в которых утверждается, что с вероятностью, как угодно близкой к единице, выполняются определенные соотношения.
| Неравенство Чебышева | Вероятность того, что отклонение случайной величины 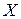 от ее математического ожидания по абсолютной величине меньше положительного числа от ее математического ожидания по абсолютной величине меньше положительного числа 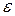 , не меньше разности между единицей и дробью, числитель которой – дисперсия случайной величины , не меньше разности между единицей и дробью, числитель которой – дисперсия случайной величины 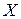 , а знаменатель – квадрат , а знаменатель – квадрат 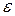
|
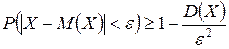 .
.
| Теорема Чебышева | Если дисперсии попарно независимых случайных величин 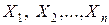 ограничены одной и той же постоянной ограничены одной и той же постоянной 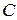 , а число их достаточно велико, то как бы ни было мало положительное число , а число их достаточно велико, то как бы ни было мало положительное число 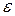 , вероятность того, что отклонение средней арифметической этих случайных величин от средней арифметической их математических ожиданий меньше по абсолютной величине , вероятность того, что отклонение средней арифметической этих случайных величин от средней арифметической их математических ожиданий меньше по абсолютной величине 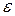 , будет как угодно близка к единице , будет как угодно близка к единице
|
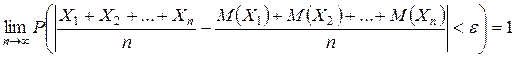 .
.
Другими словами, среднее арифметическое достаточно большого числа независимых случайных величин утрачивает характер случайной величины. На теореме Чебышева основан выборочный метод в статистике, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят о всей генеральной совокупности исследуемых объектов.
| Теорема Бернулли | Если в каждом из 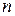 независимых испытаний вероятность независимых испытаний вероятность 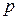 появления события появления события 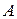 постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности 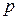 по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико
|
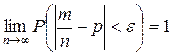 .
.
Другими словами, частость приближается при большом числе испытаний к вероятности.
Закон больших чисел лежит в основе различных видов страхования (страхование жизни человека на всевозможные сроки, имущества и др.) При планировании ассортимента товаров широкого потребления учитывается спрос на них населения. В этом спросе проявляется действие закона больших чисел. Сумма конечного числа независимых нормально распределенных случайных величин распределена по нормальному закону.
Дата добавления: 2015-10-13; просмотров: 1501;
