Конкретные законы распределения
Каждый закон распределения определяется плотностью вероятности, интегральной функцией, числовыми характеристиками и вероятностью попадания на интервал.
Биномиальный закон – это распределение вероятностей, определяемых по формуле Бернулли. Он рассчитан на дискретные величины и определяется следующими характеристиками.
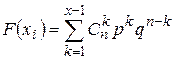 ,
, 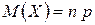
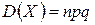 ,
, 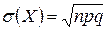
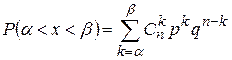 .
.
Закон Пуассона – это распределение вероятностей, определяемых по формуле Пуассона. Он характеризует дискретные величины и определяется такими величинами:
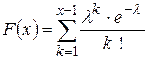 ,
, 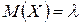 ,
,
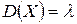 ,
, 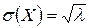 ,
, 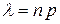 ,
,
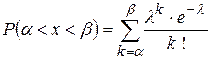 .
.
Закон равномерного распределения вероятностей – это такой закон распределения непрерывной случайной величины, все значения которой лежат на отрезке 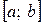 и имеют постоянную плотность вероятности на этом отрезке.
и имеют постоянную плотность вероятности на этом отрезке.
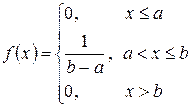
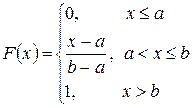
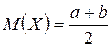 ,
, 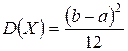 ,
, 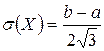 .
.
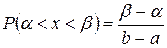 .
.
Нормальное распределение – это распределение вероятностей непрерывной случайной величины, которое описывается дифференциальной функцией
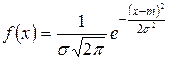 ,
,
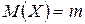 ,
, 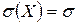 .
.
Интегральная функция нормального распределения:
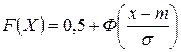 .
.
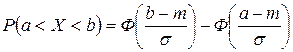 ,
,
где 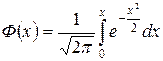 – функция Лапласа (интеграл вероятностей).
– функция Лапласа (интеграл вероятностей).
Нормальной кривой называют график плотности нормального распределения.
Вероятность заданного отклонения 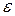 :
:
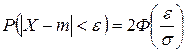 .
.
| Правило “трех сигм”: | Практически достоверным является событие, состоящее в том, что абсолютная величина отклонения нормально распределенной случайной величины от ее математического ожидания не превосходит утроенного среднего квадратического отклонения |
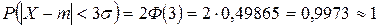 .
.
Показательное (экспоненциальное) распределение описывается дифференциальной функцией
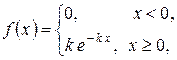
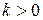 .
.
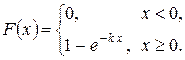
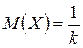 ,
, 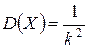 ,
, 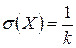 .
.
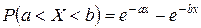 .
.
| Пример 16. | В цехе 4 мотора. Для каждого мотора вероятность того, что он включен в данный момент, равна 0,6. Составить ряд распределения числа моторов, включенных в данный момент. Найти 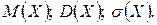
|
Решение.
Случайная величина 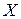 – число включенных моторов – может принимать значения 0, 1, 2, 3, 4. Для каждого возможного значения случайной величины найдем вероятность по формуле Бернулли:
– число включенных моторов – может принимать значения 0, 1, 2, 3, 4. Для каждого возможного значения случайной величины найдем вероятность по формуле Бернулли:
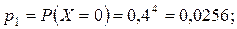
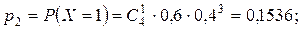
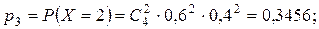
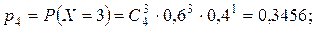
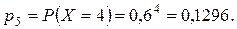
Составим ряд распределения:
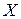
| |||||
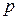
| 0,0256 | 0,1536 | 0,3456 | 0,3456 | 0,1296 |
Проверка: 0,0256 + 0,1536 + 0,3456 + 0,3456 + 0,1296 = 1.
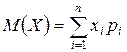 =
= 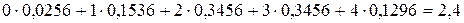 .
.
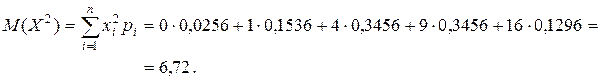
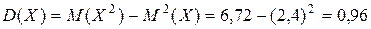 .
.
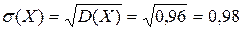 .
.
| Пример 17. | Дана интегральная функция:
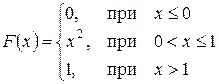 Найти:
а) дифференциальную функцию;
б) вероятность попадания случайной величины в интервал (1/4; 2/3);
в)
Найти:
а) дифференциальную функцию;
б) вероятность попадания случайной величины в интервал (1/4; 2/3);
в) 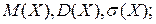 г) построить график
г) построить график 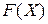 и и 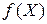 . .
|
Решение.
а) Найдем дифференциальную функцию:

б) 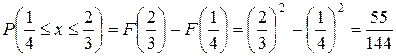 .
.
в) 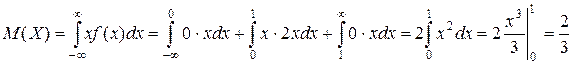 ,
,
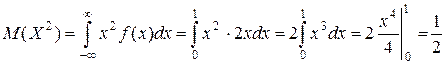 ,
,
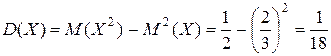 .
.
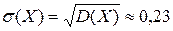 .
.
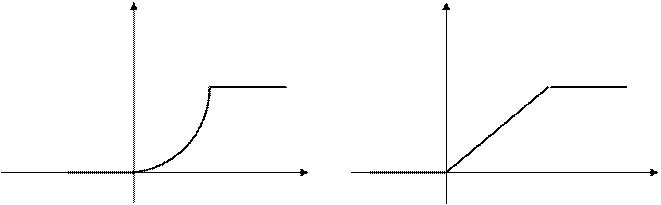
г) графики функций 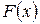 и
и 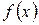 имеют вид (рис. 1, 2):
имеют вид (рис. 1, 2):
| 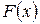
| 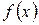
| ||||||||||||||||||||||||||
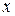
| 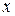
| |||||||||||||||||||||||||||
Рис. 1 Рис. 2
Дата добавления: 2015-10-13; просмотров: 1145;
