Понятие о случайных величинах
Случайной величиной называют такую переменную, которая в результате испытания может принимать одно из возможных значений, причем заранее неизвестно, какое именно. Например, число попаданий при пяти выстрелах, рост человека.
Дискретной (прерывной) называется случайная величина, которая может принимать лишь отдельные, изолированные друг от друга значения из некоторого промежутка. Например, число очков при подбрасывании игральной кости.
Непрерывной называется случайная величина, которая может принимать любое значение из некоторого интервала. Например, расстояние, которое пролетает снаряд.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и их вероятностями.
Закон распределения можно задать табличным, графическим, аналитическим способами.
Ряд распределения – это перечень всех возможных значений дискретной случайной величины и соответствующих им вероятностей.
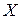
| 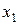
| 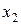
| … | 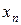
|
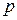
| 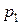
| 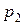
| … | 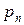
|
Сумма вероятностей всех возможных значений дискретной случайной величины равна единице
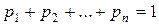 .
.
В целях наглядности ряд распределения дискретной случайной величины можно изобразить графически, для чего в прямоугольной системе координат строят точки 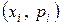 и соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения или полигоном.
и соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения или полигоном.
2. Функции распределения
Дискретные и непрерывные случайные величины можно задавать с помощью интегральной функции распределения.
Интегральной функцией распределения (или функцией распределения) называется функция 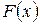 , которая определяет для каждого значения
, которая определяет для каждого значения 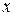 вероятность того, что случайная величина
вероятность того, что случайная величина 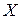 примет значение, меньшее числа
примет значение, меньшее числа 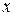
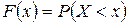 .
.
Дата добавления: 2015-10-13; просмотров: 1098;
