Локальная теорема Лапласа
Если вероятность появления события  в каждом испытании постоянна и равна
в каждом испытании постоянна и равна 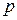 (причем
(причем 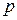 не близко к 0 и 1), то вероятность того, что событие
не близко к 0 и 1), то вероятность того, что событие  в серии из
в серии из 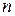 независимых испытаний (где
независимых испытаний (где 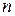 достаточно велико) появится ровно
достаточно велико) появится ровно 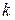 раз, определяется по приближенной формуле:
раз, определяется по приближенной формуле:
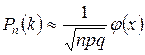 ,
, 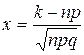 ,
,
где 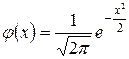 – функция вероятностей,
– функция вероятностей, 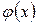 – четная функция.
– четная функция.
Значения функции 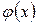 находят по таблице (приложение 1). Для всех
находят по таблице (приложение 1). Для всех 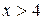
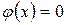 .
.
Интегральная теорема Лапласа
Если число независимых испытаний 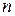 достаточно велико, а вероятность
достаточно велико, а вероятность 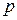 появления события
появления события  в каждом испытании не мала, то вероятность появления события
в каждом испытании не мала, то вероятность появления события  в интервале от
в интервале от 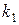 до
до 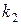 раз определяется приближенной формулой
раз определяется приближенной формулой
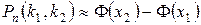 ,
,
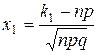 ,
, 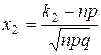 .
.
Функция 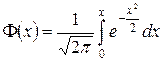 – нечетная. Значения функции
– нечетная. Значения функции 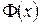 находят по таблице (приложение 2). При
находят по таблице (приложение 2). При 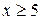
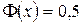 .
.
Вероятность отклонения относительной частоты от вероятности. Пусть производится 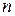 независимых испытаний, в каждом из которых вероятность появления события
независимых испытаний, в каждом из которых вероятность появления события  постоянна. Вероятность того, что в
постоянна. Вероятность того, что в 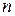 испытаниях относительная частота появления события
испытаниях относительная частота появления события  отклонится от вероятности не более, чем на
отклонится от вероятности не более, чем на 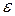 , определяется приближенной формулой
, определяется приближенной формулой
.
Наивероятнейшее число появлений события в серии независимых испытаний. Числопоявлений события в
в 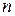 независимых испытаниях
независимых испытаниях 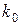 называется наивероятнейшим, если вероятность появления события это число раз является наибольшей.
называется наивероятнейшим, если вероятность появления события это число раз является наибольшей.
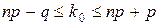 .
.
Если:
§ 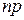 – целое число, то
– целое число, то 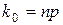 ,
,
§ 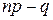 – дробное число, то существует единственное число
– дробное число, то существует единственное число 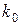 , равное целой части
, равное целой части 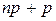 ,
,
§ 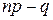 – целое число, то существует два наивероятнейших числа, равные соответственно левой и правой части неравенства.
– целое число, то существует два наивероятнейших числа, равные соответственно левой и правой части неравенства.
| Пример 11. | Вероятность попадания в мишень при одном выстреле равна 0,4. Найти вероятность 3-х попаданий при 5-ти выстрелах. |
Решение.
По формуле Бернулли определим искомую вероятность
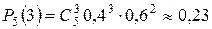 .
.
| Пример 12. | Учебник издан тиражом 100 000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Найти вероятность того, что тираж содержит ровно 5 бракованных книг. |
Решение.
По условию 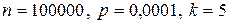 .
.
Используем формулу Пуассона.
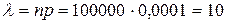 ,
,
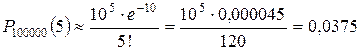 .
.
| Пример 13. | 75% всей продукции соответствует требованиям высшего сорта. Найти вероятность того, что в партии из 150 изделий: а) 100 изделий окажется высшего сорта; б) не менее 110 изделий окажутся высшего сорта. |
Решение.
а) 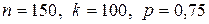 .
.
Событие  – появление изделия высшего сорта.
– появление изделия высшего сорта.
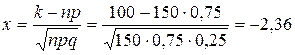 .
.
По таблице (приложение 1) находим:
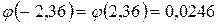 ,
,
тогда
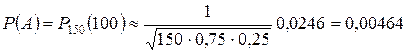 .
.
б) 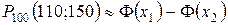 .
.
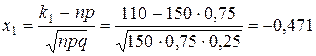 ,
,
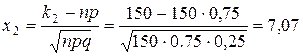 ,
,
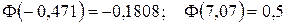 .
.
Значит
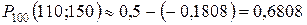 .
.
| Пример 14. | Вероятность появления события в каждом из 625 независимых испытаний равна 0,8. Найти вероятность того, что относительная частота отклониться от 0,8 не более, чем на 0,04. |
Решение.
.
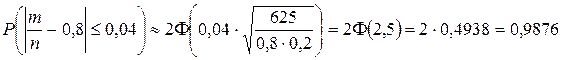 .
.
| Пример 15. | Вероятность того, что деталь стандартна, равна 0,9. Сколько необходимо проверить деталей, чтобы с вероятностью 0,9544 можно было утверждать, что частость отклониться от вероятности не более, чем на 0,02. |
Решение.
.
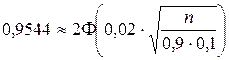 ,
, 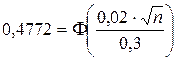 ,
,
по таблице 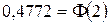 ,
,
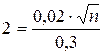 ,
, 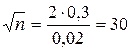 ,
, 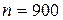 .
.
Дата добавления: 2015-10-13; просмотров: 1252;
