Формула Бейеса
Если событие  уже произошло, то переоценить вероятность каждой гипотезы можно по формуле Бейеса.
уже произошло, то переоценить вероятность каждой гипотезы можно по формуле Бейеса.
Имеется полная группа несовместных гипотез 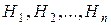 . Вероятности этих гипотез до опыта известны и равны
. Вероятности этих гипотез до опыта известны и равны 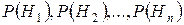 . Произведен опыт, в результате которого появилось событие
. Произведен опыт, в результате которого появилось событие  . Вероятность гипотезы
. Вероятность гипотезы 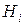 при условии наступления события
при условии наступления события  определяется формулой
определяется формулой
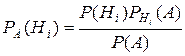 ,
, 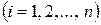 ,
,
где 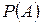 – полная вероятность события
– полная вероятность события  .
.
| Пример 6. | Вероятность попасть в мишень для первого стрелка равна 0,9, для второго – 0,8. Оба стрелка выполнили по одному выстрелу. Определить вероятность того, что мишень поражена. |
Решение.
Событие 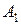 – попадание первого стрелка, событие
– попадание первого стрелка, событие 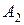 – попадание второго стрелка.
– попадание второго стрелка.
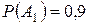 ,
, 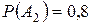 .
.
Событие 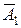 – промах первого стрелка, событие
– промах первого стрелка, событие 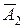 – промах второго стрелка.
– промах второго стрелка.
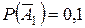 ,
, 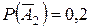 .
.
Событие  – мишень поражена, хотя бы один стрелок попал.
– мишень поражена, хотя бы один стрелок попал.
Событие 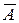 – оба стрелка промахнулись.
– оба стрелка промахнулись.
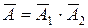 .
.
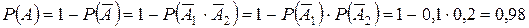
| Пример 7. | В одной урне 2 белых, 4 красных и 3 черных шара, в другой соответственно 3, 2 и 5 шаров. Вынимают по одному шару из каждой урны. Определить вероятность того, что они разные. |
Решение.
В урнах содержатся шары трех цветов. Варианты разных по цвету шаров могут быть такими:
| 1 урна | б | б | к | к | ч | ч |
| 2 урна | к | ч | б | ч | б | к |
Вероятность каждого из вариантов определяется по теореме умножения вероятностей независимых событий, а общая вероятность – их суммированием.
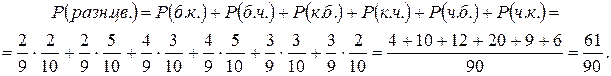
| Пример 8. | Вероятность одного попадания в цель при одном залпе из двух орудий равна 0,44. Найти вероятность поражения цели при одном выстреле первым из орудий, если известно, что для второго орудия эта вероятность равна 0,6. |
Решение.
Обозначим вероятности попадания 1-го и 2-го орудия через 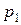 и
и 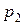 , тогда вероятности противоположных событий будут
, тогда вероятности противоположных событий будут 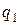 и
и 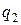 , а вероятность только одного попадания выразится соотношением:
, а вероятность только одного попадания выразится соотношением:
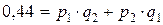 ;
; 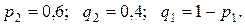
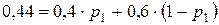 ,
,
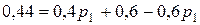 ,
,
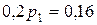 ,
,
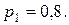
| Пример 9. | На склад поступают утюги с двух заводов, первый из которых поставляет 70%, второй – 30% всего количества. Известно, что первый завод выпускает 90% продукции, способной прослужить гарантийный срок, а второй – 95%. Какова вероятность, что наугад взятый утюг прослужит гарантийный срок? |
Решение.
Событие  – утюг прослужит гарантийный срок.
– утюг прослужит гарантийный срок.
1. Определение гипотез:
гипотеза 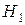 – утюг изготовлен первым заводом,
– утюг изготовлен первым заводом,
гипотеза 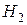 – утюг изготовлен вторым заводом.
– утюг изготовлен вторым заводом.
Гипотезы несовместны и образуют полную группу.
2. Определение доопытных вероятностей гипотез
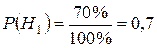 ;
; 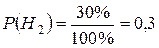 .
.
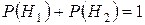 .
.
3. Определение условных вероятностей
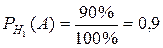 ;
; 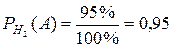 .
.
4. Определение полной вероятности
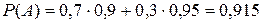
| Пример 10. | Есть 10 урн. В 3-х из них – по 4 белых, 6 черных шаров, в 5-ти – по 7 белых, 3 черных шаров, в 2-х – по 2 белых, 8 черных шаров. Наугад взятый шар оказался белым. Какова вероятность того, что он взят из 3-й группы урн? |
Решение.
Здесь, очевидно, нужно использовать формулу Бейеса, т.к. результат известен (шар оказался белым).
Событие  – шар оказался белым.
– шар оказался белым.
1. Гипотеза 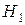 – шар взят из первой группы урн.
– шар взят из первой группы урн.
Гипотеза 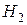 – шар взят из второй группы урн.
– шар взят из второй группы урн.
Гипотеза 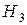 – шар взят из третьей группы урн.
– шар взят из третьей группы урн.
Гипотезы несовместны и образуют полную группу.
2. 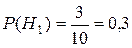 ;
; 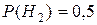 ;
; 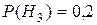 ;
; 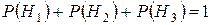 .
.
3. 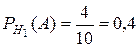 ;
; 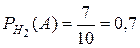 ;
; 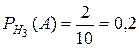 .
.
4. 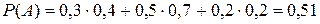 .
.
5. 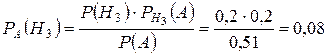 .
.
Дата добавления: 2015-10-13; просмотров: 855;
