Барометрична формула
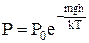
визначає залежність тиску атмосфери Р від висоти h над Землею. Щоб знайти цю формулу приймемо, що на поверхні Землі атмосферний тиск 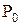 , а на при поверхневих висотах температура є сталою (величина зміни DТ з висотою мала порівняно з Т на поверхні Землі). Газ атмосфери можна описати рівнянням Клапейрона- Менделєєва, визначивши з нього, наприклад, густину повітря
, а на при поверхневих висотах температура є сталою (величина зміни DТ з висотою мала порівняно з Т на поверхні Землі). Газ атмосфери можна описати рівнянням Клапейрона- Менделєєва, визначивши з нього, наприклад, густину повітря
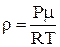 . (1)
. (1)
Нехай на висоті h тиск Р. При збільшенні висоти на dh тиск зменшиться на величину тиску стовпа повітря dP=-rgh. П і с л я
підстановки виразу для густини одержимо
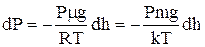 . (2)
. (2)
З останнього виразу можна одержати диференціальне рівняння для тиску з розділеними змінними Р та h
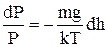 . (3)
. (3)
Після інтегрування маємо
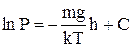 . (4)
. (4)
Сталу С знайдемо з умови, що на висоті h = 0 тиск P = 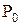 і остаточно
і остаточно
Р = 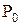
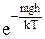 . (5)
. (5)
Одержаний вираз називається барометричною формулою.
Для вимірювання тиску використовують прилад, який називається барометром. Барометр, проградуйований за барометричною формулою у значеннях висоти, називається альтиметром. За допомогою альтиметра можна вимірювати висоту підйому над поверхнею Землі.
6.10.2. Розподіл Больцмана
Залежність тиску атмосфери Землі від температури можна наблизити формулою для тиску ідеального газу P=nkT. Якщо знехтувати зміною температури, то концентрація частинок буде функцією лише тиску Р і тоді для концентрації n можна записати
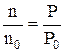 , (6)
, (6)
де 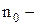 концентрація при тискові
концентрація при тискові 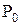 . Підставляючи (6) у (5) барометричної одержимо вираз
. Підставляючи (6) у (5) барометричної одержимо вираз
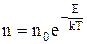 , (7)
, (7)
де Еп = mgh ¾ потенціальна енергія частинки в полі тяжіння Землі.
Вираз (7) представляє розподіл частинок у потенціальному полі в залежності від їх потенціальної енергії. Цей розподіл називається розподілом Больцмана.
6.11. Розподіл Максвелла - Больцмана
6.11.1. Розподіл Максвеллаза значеннями кінетичної енергії
для частинок ідеального газу має вид
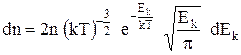 ,
,
де dn ¾ число частинок із загальної їх кількості n, кінетичні енергії яких лежать в інтервалі ( 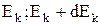 ).
).
Цей розподіл можна одержати, якщо в розподілі по швидкостям провести заміну змінної
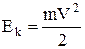 ,
, 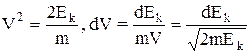 .
.
Підставивши ці вирази в розподіл Максвелла, одержимо
dn = 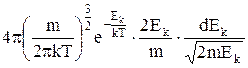 ,
,
і остаточно
dn = 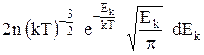 .
.
Функція розподілу матиме вигляд
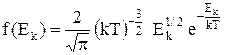 .
.
6.11.2. Розподіл Максвелла - Больцмана
для частинок у потенціальному полі з енергією Еп
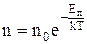 ,
,
можна об'єднати із розподілом Максвелла в один розподіл Максвелла-Больцмана, який визначає число частинок в одиниці об'єму, що знаходяться в потенціальному полі з енергією Е і мають швидкість в інтервалі [V,V+dV]. Цей розподіл має вигляд
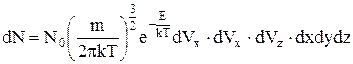 ,
,
де 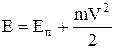 ¾ повна енергія частинки, N0 - загальне число частинок. Потенціальна енергія частинки залежить від координати
¾ повна енергія частинки, N0 - загальне число частинок. Потенціальна енергія частинки залежить від координати 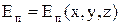 , а
, а 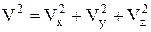 .
.
Дата добавления: 2015-09-18; просмотров: 3398;
