Шкала Фаренгейта

.

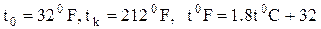3).Шкала температури Кельвіна

.

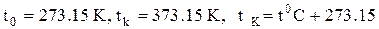T = 0 K є температура абсолютного нуля ¾ температура, при якій припиняється будь-який рух атомів чи молекул будь - яких речовин, а у кристалах відбуваються нульові коливання решітки.

4).Абсолютна термодинамічна шкалавизначається шляхом порівняння температур тіл нагрівача та холодильника в оборотному циклі Карно через виміряні кількості відданого нагрівачем робочому тілу тепла Q_н й одержаного тепла холодильником Q_х

.

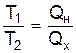Прийнято вважати, що атмосфера Землі має нормальні умови, коли

-тиск 101.33 кПа (760 мм рт. ст.),

-температура 273.15 К,

-об'єм моля ідеального газу 22.41·10^-3 м³·моль^-1.

6.4. Енергія частинки ідеального газу

6.4.1.Теорема Больцмана про рівнорозподіл енергії. Енергія частинки

В п.2.9 введено поняття ступенів свободи, зв'язків та узагальнених координат системи з N частинок. Молекула має усього 3N ступенів свободи. Для молекули з пружнними зв'язками між атомами вказано, що вона має 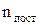=3 поступальні ступені свободи ¾ координати X,Y,Z положення центра мас у просторі, 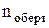=3 обертові ступені свободи ¾ кути a, b, g, що визначають орієнтацію молекули відносно осей OX,OY,OZ. Інші 3n-( 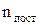+ n_оберт) ступені свободи є коливальними ступенями свободи.

Зв'язки між атомами в молекулі, наприклад, води Н₂О при кімнатних температурах можна вважати жорсткими, тому що при таких температурах теплової енергії замало для збурення коливань між атомами. При високих температурах такі збурення можуть відбуватися і зв'язки стануть коливальними ступенями свободи. Якщо система частинок є лінійною, то обертання навколо осі, що проходить через частинки, не змінює положення частинок і тоді .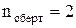

Теорема Больцмана про рівнорозподіл енергіїза ступенями свободи установлює, що на кожну поступальну або обертову ступінь свободи приходиться енергія kT/2, а на коливальну ступінь ¾ kT (коливальна ступінь характеризується наявністю кінетичної ¾ kT/2 та потенціальної ¾ kT/2 енергій).

Внутрішня теплова енергія молекулиз N атомами визначається як

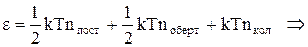
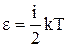, (3)

де

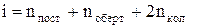
де n_пост - число поступальних, n_оберт ¾ число обертових і n_кол ¾ число коливальних ступенів свободи. Зауважимо, що n_пост + n_оберт + n_кол = 3N. Для звичайних температур теплової енергії kТ недостатньо для теплових збуджень коливань у молекулі і тому покладається, що зв'язки частинок у молекулі жорсткі і n_кол = 0.

6.5. Внутрішня енергія ідеального газу

Внутрішня теплова енергіяідеального газу. Якщо частинка має масу m₀, а газ має - m, то він має 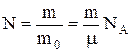частинок, а його внутрішня енергія теплового руху дорівнює

,

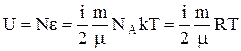де 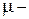молярна маса, або

U = 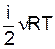. (4)

Якщо врахувати, що стан ідеального газу визначається рівнянням Клапейрона-Менделєєва

,

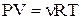то вираз для внутрішньої енергії прийме вид

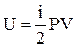. (5)

6.6. Молекулярно кінетична теорія для тиску

Якщо на плоску поверхню площею DS з нормаллю 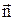діє сила 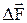, то під тискомР розуміють границю відношення величини нормальної складової сили 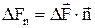до DS

.

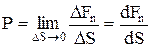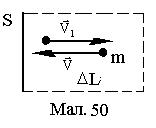Співударяючись із стінками посудини, в якій знаходиться ідеальний газ, частинки створюють середню силу <F> дії на одиницю поверхні, тобто створюють тиск Р. Як показав Максвел, цей тиск не залежить від того, що співударяння з стінками пружні чи не пружні. Знайдемо тиск газу у наближенні абсолютно пружного співударяння частинок із стінкою. Для цього покладемо, що частинка перед ударом має швидкість 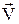, котра направлена перпендикулярно поверхні стінки (див.Мал.50). Після абсолютно пружного співударяння, частинка змінить напрямок швидкості на протилежний і її приріст імпульсу складатиме

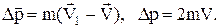
Якщо концентрація частинок дорівнює n, то у поперечному напрямку до стінки буде рухатися n/6 частинок (маємо один з 6 напрямків декартових координат). За час Dt стінки досягнуть усі частинки, котрі знаходяться на відстані від неї DL=VDt. Якщо розглянути одиничну поверхню DS, то за цей час із стінкою співударяться

DN=nDSDL/6. (1)

частинок і стінці буде передано імпульс

DP=DN×Dp=2mV×nDSVDt/6=nmV²Dt/3. (2)

За другим законом Ньютона на стінку буде діяти сила

.

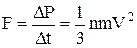Знайдемо середню силу <F>=n<mV²>/3, що діє 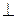на стінку одиничної площі

DS і фактично є тиском Р, який створюється частинками газу, тобто

Р=n<mV²>/3.

Величина <mV²>/2 є середньою кінетичною енергією теплового руху частинки. Якщо газ одноатомний з і=3, то, враховуючи 6.4.2. (3), одержимо

<mV²>=3kT

і тоді

P=nkT. (3)

6.7. Ефективний діаметр та ефективний переріз розсіювання

Знаходячись у неперервному тепловому русі частинки газу співударяються, змінюючи напрямок руху і швидкість. У цьому питанні важливим для розгляду розсіювання є оцінка динамічного розміру частинки.

Ефективним діаметром 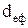частинок ідеального газу є найменша відстань між центрами двох частинок, які здійснюють центральний пружний удар. За порядком величини

.

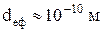Нижче в Таблиці 1 наведені значення ефективного діаметра для деяких газів.

Таблиця 1. Значення ефективного діаметра деяких молекул

Ефективний газокінетичний поперечний перерізs_еф дорівнює площі круга з радіусом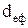

.

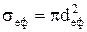Властивістю ефективного перерізу є те, що дві частинки, які одночасно проходять через 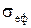, обов'язково співударяються.

6.8. Кінематичні характеристики ідеального газу

6.8.1. Статистичний розподіл частинок за напрямком руху

Хаотичність теплового рухуn частинок ідеального газу означає їх рівнорозподіл руху за напрямками швидкостей, а саме: усі напрямки теплового руху рівно ймовірні. Якщо в простір частинок увести декартову систему координат із 3-ма осями ¾ x, y, z і 6-ма напрямками по ним (±), то в кожному з них рухається

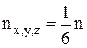
частинок. Наприклад, якщо частинки мають середню швидкість теплового руху V, то в додатному напрямку осі ОХ через перпендикулярну до неї площину S за час dt пройдуть всі частинки, що знаходяться на відстані dL = V·dt в об'ємі dL×S, а їх загальне число становить

.

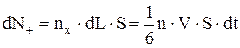6.8.2. Число зіткнень частинки за одиницю часу

Число співударяньчастинки із середньою швидкістю V при концентрації n за 1с дорівнює

.

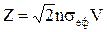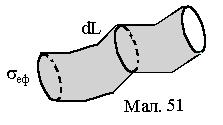Щоб одержати цей вираз, розглянемо траєкторію, що її опише частинка ідеального газу за час dt. Вона являє собою деяку ламану лінію, у вузлах якої відбулися зіткнення з іншими частинками. ЇЇ довжина становить dL=Vdt. Побудуємо на цій ламаній, як на осі, циліндр з основою, рівною ефективному перерізу 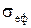(див.Мал.51)). Приймаючи до уваги властивість ефективного перерізу, можна стверджувати, що розглядувана частинка обов’язково співудариться з усіма нерухомими частинками

,

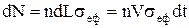які знаходяться в циліндрі. Але частинки рухаються і тому замість швидкості V потрібно взяти відносну середню квадратичну швидкістьV_в, яку розрахуємо так

.

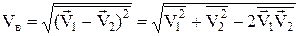В записаному виразі 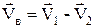¾ вектор відносної швидкості двох частинок. З достатньою точністю можна покласти, що 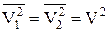, а 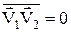тому, що кут 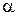між векторами 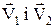змінюється в межах від 0⁰ до 180⁰ і 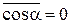. В результаті маємо, що 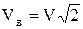і число співударянь за час dt дорівнює 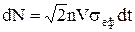, а число співударянь за одиницю часу дорівнює

.

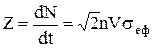За нормальних умов частинка атмосфери з 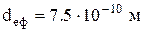здійснює

Z=3,1×10¹⁰ с^-1.

6.8.3. Середня довжина вільного пробігу

Середня довжина вільного пробігуl є середня відстань між двома послідовними співударяннями частинок, що рухаються рівномірно й прямолінійно. Величину l можна обчислити, виходячи з того, що на довжині траєкторії dL=Vdt відбувається Zdt співударянь і тоді середня довжина вільного пробігу між співударяннями становить

.

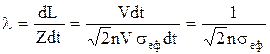Приймаючи до уваги, що 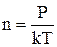, можна записати

.

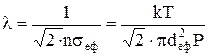За нормальних умов частинка атмосфери з 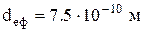має .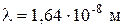

6.9. Розподіл Максвелла для частинок за швидкостями

6.9.1. Закон розподілу

частинок ідеального газу за швидкостями визначає їх стаціонарний розподіл за швидкостями в умовах термодинамічної рівноваги й відсутності зовнішнього силового поля.

Розподіл частинок ідеального газу за абсолютними значеннями швидкостей V дослідив Максвелл. Він визначив, що число частинок, швидкості яких лежать в інтервалі (V; V + dV) представляється виразом

,

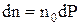де 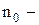загальне число частинок, а їх частка

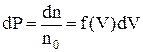(1)

є ймовірністю такого розподілу із густиною

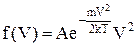. (2)

В цьому виразі m ¾ маса частинки, k ¾ стала Больцмана, Т ¾ температура. Стала нормування А визначається так

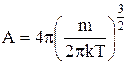. (3)

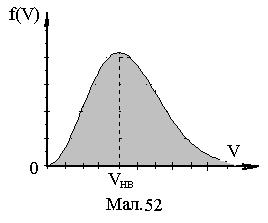
Залежність (2) представлена на Мал.52.

Закон Максвелла можна застосовувати і для скінчених малих величин 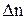та

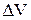
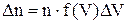. (4)

6.9.2. Максимум густини розподілу

f(V) знаходиться в точці V=V_нв (див.Мал.5), яка називається найбільш імовірною швидкістюі

.

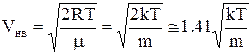Дійсно,

.

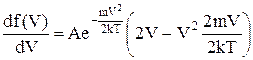Прирівняємо похідну 0 і знайдемо точку екстремуму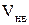

,

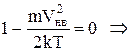
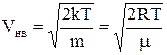що й треба було довести.

Вираз 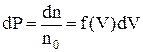значно спрощується, якщо ввести змінну

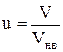, тоді , ,

, .

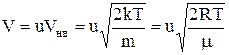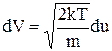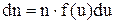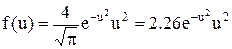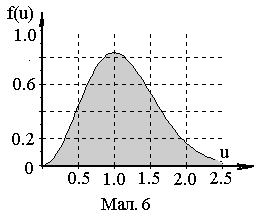
Графік густини розподілу f(u) по u представлено на Мал.6. Максимум густини такого розподілу приходиться на u=1.

6.9.3. Середня арифметична швидкість

визначається як

,

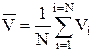для дискретних значень V та

,

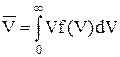для неперервних значень V.

Розрахунки середньої швидкостічастинок ідеального газу за розподілом Максвелла дають

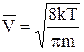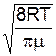= »1. 60 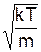. (1)

Дійсно,

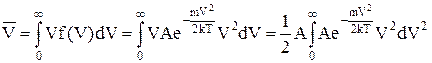
Зробимо заміну змінної

, ,

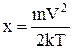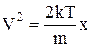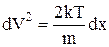
i тепер

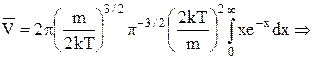
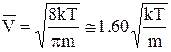. (2)

Ми проінтегрували

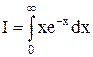
по частинам:

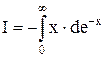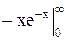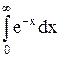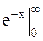= + =0- =1.

6.9. 4. Середня квадратична швидкістьвизначається як

с = 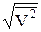, (1)

де 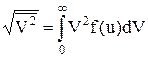. Розрахуємо (1) за допомогою теореми Больцмана про рівнорозподіл енергії за ступенями свободи для вільної частинки. Згідно цієї теореми середня кінетична енергія теплового руху частинки з масою m дорівнює

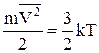
і звідси

с = .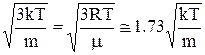

6.9.5. Експериментальна перевірка розподілу Максвелла

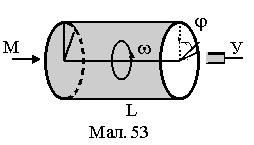
була зроблена лише через 60 років після його встановлення О. Штерном та іншими дослідниками. Зокрема, найбільш простий та надійний дослід по вимірюванню середньої швидкості частинок та їх розподіл провів Б. Ламмерт. Вузький молекулярний пучок М (див.Мал.53) вирізувався системою діафрагм в парах металу, які виходили з молекулярної печі ¾ посудини, в якій випаровувався рідкий метал. Цей пучок проходив через два диски з вузькими радіальними прорізами, паралельно осі, на якій знаходились диски. Напроти пучка розміщувався уловлювач У. Прорізи були повернуті один відносно другого на кут j. При нерухомих дисках пучок не потрапляв в уловлювач, а при обертанні з кутовою швидкістю w вони проходили вільно. Це означало, що час повороту дисків на кут j дорівнював часу прольоту частинок відстані L між дисками: 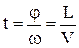, де V ¾ середня швидкість молекул при заданій температурі Т. Звідси маємо

.

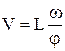6.10. Барометрична формула та розподіл Больцмана