Ідеальний газта його характеристики
Вступ
Молекулярна фізика¾ наука, що вивчає фізичні властивості та агрегатні стани речовини в залежності від її молекулярної будови, сил взаємодії між структурними частинками - атомами чи молекулами та характеру теплового руху цих частинок. Молекули складаються з атомів. У складі атомів є однакове число електронів і протонів, та нейтрони. Протони та нейтрони утворюють ядро атома. Іонявляє собою заряджений атом.
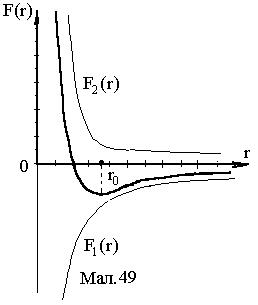
На малих відстанях між частинками речовини (r~10-9 м) виникає сила притягання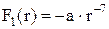 
, апри ще менших відстанях виникає сила відштовхування 
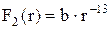. Ці сили прикладені до частинки, лежать на одній прямій і протилежно направлені. На відстані 
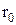рівнодійна сил 
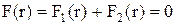і точка з координатою 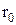є точкою рівноваги. При малих відхиленнях від положення рівноваги, рівнодійна сила лінійно залежить від г і може створювати коливальний рух. На Mал.49 наведена залежність рівнодійної сили в залежності від відстані між частинками.
Велике число частинок речовини досліджується статистичним методом. Статистичний метод- метод, що вивчає властивості макроскопічних систем на підставі ймовірнісного та статистичного аналізу закономірностей теплового руху великого числа мікрочастинок, що складають ці системи. За допомогою молекулярно-кінетичної теорії визначаються такі властивості термодинамічних систем
· тиск,
· температура,
· енергія,
· теплоємність,
· явища переносу та інше.
В основі молекулярно-кінетичної теоріїлежать три положення:
* усі фізичні тіла складаються з великого числа частинок ¾ молекул, атомів або іонів, розміри яких складають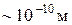 
,
* частинки речовини постійно знаходяться в тепловому хаотичному русі, а їх середня кінетична енергія визначає температуру тіла,
* між частинками речовини діють сили взаємодії, які, в залежності від відстані між частинками, будуть силами тяжіння або силами відштовхування.
6.2. Імовірністьта флуктуації
Наведемо деякі визначення поняття ймовірності.
1. Імовірність wі деякого і-го стану системи визначається границею відношення часу tі, на протязі якого система знаходиться в даному стані, до повного часу Т спостереження за системою при необмеженому збільшенні Т
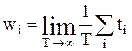. (1)
2. Якщо фізична величина А при N вимірюваннях мала Ni число значень Аі, то ймовірність wi того, що величина А має значення Аі дорівнює границі відношення Ni/N при необмеженому зростанні N і вона співпадає з імовірністю wі і - го стану системи
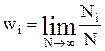. (2)
3. Імовірність dw(A) того, що фізична величина має значення в інтервалі (A; A + dA) пропорційна dA
dw(A) = f(A)dA, (3)
де f(A) - називається густиною ймовірності або функцією розподілу ймовірності.
Умова нормування ймовірностідля дискретних станів
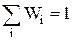(4)
¾ сума ймовірності по всім можливим станам є ймовірність достовірної величини і вона дорівнює 1, а для неперервної зміни стану сума замінюється інтегралом
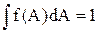(5)
¾ сума ймовірностей для всіх елементарних значень параметра стану А є ймовірність достовірної величини і дорівнює 1.
Середнє статистичне значеннявеличини А позначається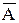 
і визначається для дискретних станів так
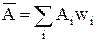, (6)
а для неперервної зміни величини А як
,
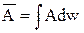де сума й інтеграл беруться по всім можливим станам системи.
Флуктуації¾це випадкові відхилення термодинамічних параметрів від рівноважних значень. Якщо термодинамічна система складається з невеликого числа частинок, то розподіл частинок, випадково відхиляючись від рівноважного, може суттєво змінювати величини термодинамічних параметрів. Для кількісної оцінки флуктуації деякої величини А використовують квадратичну флуктуацію, яку ще називають дисперсією s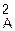 
. Дисперсія є середнє значення квадрата відхилення А від її середнього значення:
.
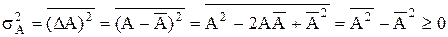Величина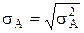 
називається абсолютною флуктуацією, а 
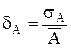¾ відносною.
Природа флуктуацій термодинамічних величин визначається хаотичним тепловим рухом структурних частинок середовища. Чим більше число N цих частинок, тим менший вплив їх флуктуацій на значення термодинамічних величин. Доведено, що для хімічно однорідного ідеального газу, при сталому об'ємі, флуктуації густини r, тиску Р та температури Т обернено пропорційні кореню з числа частинок газу
.
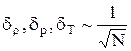Звідси видно, що для середовища з великим числом частинок флуктуаціями термодинамічних величин можна нехтувати.
Ідеальний газта його характеристики
Фізична модель ідеального газу передбачає, що
· в ньому відсутні сили притягання між частинками на відстані,
· власним об'ємом частинок газу, порівняно з наданим йому об'ємом, можна знехтувати,
· співударяння між частинками центральні й пружні.
· частинки здійснюють хаотичний тепловий рух, який відповідає рівно ймовірному напрямкові руху частинок по всім виділеним напрямкам. Наприклад, в системі координат XYZ є 6 напрямків руху і тому в напрямкові + ОХ, як і в інших напрямках, із N частинок буде рухатися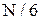 
частинок.
Молекула¾ найменша стійка частинка речовини, яка ще несе в собі її хімічні властивості.
Молекула складається з атомів хімічних елементів, наприклад, молекула кисню ¾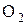 
, води ¾ 
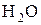, азоту ¾ 
.
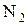Атом- найменша частинка хімічного елемента, яка є носієм його хімічних властивостей, наприклад, кисень ¾ О, водень ¾ Н, азот ¾ N.
Атомна одиниця маси(аом) ¾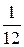 
частка маси атома стійкого ізотопу вуглецю 
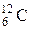і
,
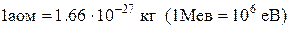яка є мірою мас атомів та молекул.
Атомна (молекулярна) масаА(М) ¾ масаатома (молекули) m виражена в атомних одиницях маси. Їх маса в системі СІ
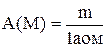
Наприклад, атомна маса водню ¾ А(Н)=1, молекулярна маса молекули водню ¾ М(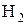 
)=2, А(N)=14, M(CO)=20, М( 
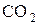)=28, а масу молекули 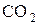можна обчислити через молярну масу у такий спосіб
.
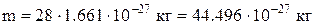Моль¾ кількість речовини, що містить у собі число Авогадро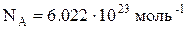 
структурних одиниць: атомів (простий хімічний елемент) або молекул (складний хімічний елемент).
Маса моляречовини m вимірюється в кг і її можна обчислити через атомну А чи молекулярну М маси так
.
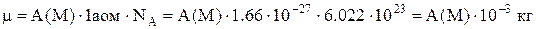Кількість моліву речовині позначається літерою n і вона дорівнює n=m/m.
Універсальна (молярна) газова стала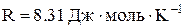 
.
Стала Больцмана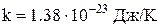 
. Величини k, NA, та R зв'язані співвідношенням 
.
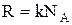Дата добавления: 2015-09-18; просмотров: 584;