Барометрична формула. Розподіл Больцмана

У разі обґрунтування розподілу молекул за швидкостями і кінетичними енергіями ми вважали, що зовнішні сили на молекули газу не діють. А як поводиться газ, що перебуває у потенціальному полі? Розглянемо це на прикладі земної атмосфери. Відомо, що атмосферний тиск зумовлений силами гравітаційного притягання, які діють на молекули повітря з боку Землі. Вважатимемо, що атмосферне повітря перебуває у стаціонарному стані, а його температура всюди однакова. За цих умов рівноважний стан довільного виділеного об’єму повітря забезпечений тим, що вага повітря зрівноважена силою Архімеда, яка зумовлена різницею тисків, що діють на нижню і верхню основи виділеного об’єму. Водночас молекули повітря перебувають у хаотичному безупинному тепловому русі. Сукупна дія сили тяжіння і теплового руху молекул спричиняє нерівномірність розподілу густини атмосфери з висотою, отже атмосферний тиск з висотою h знижується. Цю залежність виражає барометрична формула, уперше отримана П. Лапласом 1821 р.:

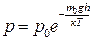, (2.25)

де р₀ – атмосферний тиск на рівні моря (h=0).

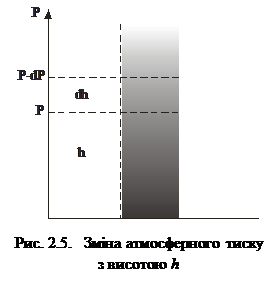
Для доведення (2.25) розглянемо статичний вертикальний атмосферний стовп повітря висоти h (рис. 2.5). Нехай на висоті h тиск повітря становить р, тоді на висоті h+dh тиск дорівнюватиме

р-dp. Оскільки в шарі товщиною dh густину повітря можна вважати сталою, то приріст тиску

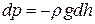. (2.26)

Якщо тепер скористатись рівнянням стану газу p=nkT і врахувати, щ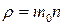о , то 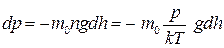, звідки

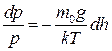. (2.27)

Проінтегруємо (2.27) в межах від р₀ до р і від 0 до h, отримаємо формулу Лапласа (2.25). Якщо тепер знову скористатись рівнянням стану газу 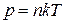то (2.25) можна звести до вигляду

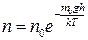, (2.28)

де n – концентрація молекул на висоті h, n₀ – концентрація молекул на рівні h=0.

Зазначимо, що m₀gh – це потенціальна енергія молекул повітря у полі сили земного тяжіння. Больцман довів, що залежність (2.28) характерна для будь-якого газу, який перебуває у потенціальному полі

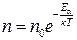. (2.29)

Розподіл Больцмана (2.29) описує рівноважний розподіл за потенціальною енергією молекул газу, що перебувають у зовнішньому потенціальному полі сил.

Якщо концентрація частинок невідома в жодній точці поля, але відома загальна кількість частинок N, то розподіл Больцмана записують у вигляді

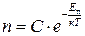. (2.30)

Нормувальний множник С знаходять з умови нормування

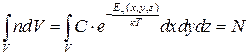, (2.31)

де V – об’єм, у якому містяться частинки.